Замощення площини Лобачевського правильними трикутниками
Припустимо, у нас є точка А. Задача замощення площини правильними трикутниками полягає у побудові максимальної кількості правильних трикутників так, щоб у кожного одна вершина
лежала в точці А, а дві сторони були суміжними із сусідніми трикутниками.
У евклідовій геометрії, очевидно, максимальна кількість таких трикутників дорівнює шести, так як всі
кути трикутника дорівнюють 60°. На площині Лобачевського ця кількість дорівнює
семи. Це цікаве явище ілюструє наступна модель.(див. файл Гіперболічна геометрія.ggb.) Цьому цікавому явищу присвячена наступна побудова.
Задача на побудову 1. Побудувати модель для роботи з гіперболічною площиною та розробити набір користувальницьких інструментів для побудови об'єктів у площині Лобачевського.
Проаналізуємо одержану модель.
Довжини сторін і кути у
трикутників рівні між собою, проте нам вдалося замостити сім'ю правильними
трикутниками коло в 360°.
Отже, на площині Лобачевського у правильного трикутника
сума всіх його кутів менша за180°.
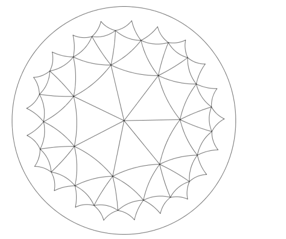
Цю побудову можна продовжувати нескінченно, повторюючи ті ж дії для побудови рядів
правильних трикутників навколо семи основних, як фрактал. Щоб почати побудову
нового ряду трикутників, необхідно побудувати гіперболічні кола, радіусом яких
служать сторони вже готових трикутників, знайти точки їх перетину і з'єднати їх
гіперболічними відрізками. На малюнку показано зображення креслення з чотирма
рядами гіперболічних трикутників.
Навчальне дослідження1. Дослідити, як
змінюється кількість трикутників в кожному ряду.
Задача на побудову 2. Створити користувацький інструмент, що дозволяє скоротити кількість необхідних кроків для побудови рядів трикутників.
Навчальне дослідження 2. На основі побудованої
моделі створіть користувацький інструмент, який будуватиме не один трикутник, а
ряд із них. Чи можливо створити один інструмент, який може побудувати ряди з 7-ми
або з 21-ого трикутника?
Навчальне дослідження 3. Створіть користувацький
інструмент, який за вказаною кількістю рядів автоматично будує замощення
площині гіперболічними трикутниками.
Нагадаємо, що теселяція – це замощення площині однорідними фігурами так, щоб не було простору між ними. Наприклад:



Навчальне дослідження 4. Завантажте декілька зображень картин з Інтернету(наприклад:
https://lenacab.livejournal.com/202252.html) в креслення GeoGebra і співставте
їх із отриманою теселяцією з гіперболічних трикутників. Сформулюйте висновки.
Приклади теселяції у мистецтві:



Відповідь
Навчальне дослідження 1:
В основі розташовано 7
трикутників, як і в другому ряду. У третьому і в четвертому рядах побудовано по
21 трикутнику. Висновок – починаючи з другого ряду, в кожному непарному ряду
трикутників буде в три рази більше, ніж у попередньому. Відповідно, в п'ятому
та шостому рядах буде по 63 гіперболічних трикутника.