Klotoida
Křivost k klotoidy je přímo úměrná délce oblouku L, tj. k = a.L. Koeficient a přímé úměrnosti je většinou velmi malý, proto je používán ve tvaru . Rovnice klotoidy vyjádřená závislostí délky s a křivostí k je tedy
.
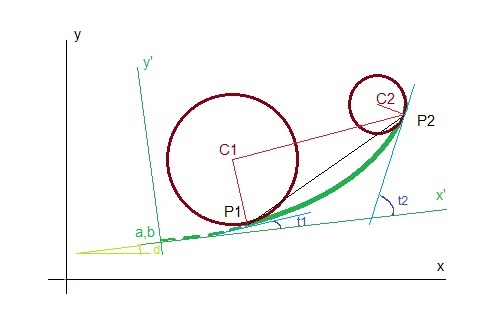
V železniční i silniční dopravě se používá pro napojení úseků s různou křivostí. Soustava souřadná je zvolena tak, že bod o křivosti 0 je v počátku, tečna v tomto bodě je osa x (přímý úsek). Pro daný koeficient přímé úměrnosti (dáno pojížděnou rychlostí) vypočítáme délku L klotoidy pro napojení na kružnicový oblouk, jenž je veden po oskulační kružnici.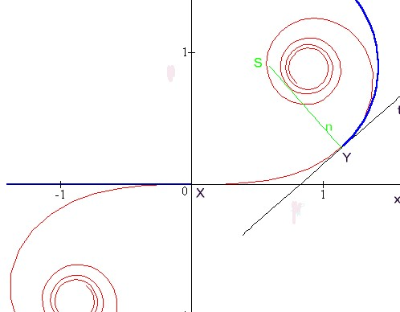
Úloha 1
Určete délku L oblouku klotoidy pro napojení přímého úseku na kruhový oblouk o poloměu r = 15 m.
Řešení: V bodě napojení musí mít klotoida i kruhová zatáčka stejnou křivost , odtud . Dosazením poloměru r=15 m získáme pro délku oblouku L =15 m.
Úloha 2: Změna směru při pohybu po klotoidě určená úhlem α
Vypočítejte odchylku přímého úseku a tečny v bodě napojení klotoidy a kruhové zatáčky r =15 m.
Řešení: Derivací parametrických rovnic klotoidy získáme jednotkový vektor tečny ve tvaru
Odtud vzorec pro úhel, který svírá tečna s osou x:
.
Po dosazení za oblouk s z předchozího příkladu . Pro hodnotu poloměru r = 15 m získáváme velikost úhlu v radiánech. α =1/2.Úloha 3: Přechodnice 3. stupně
Nahraďte klotoidu kubickou parabolou.
Řešení: Z Taylorova rozvoje 3. stupně dostáváme aproximaci ve tvaru .
Dosazením A=15 dostáváme algebraickou přechodnici třetího stupně vyjádřenou explicitně .
Úloha 4: Napojení dvou kruhových oblouků
Jak dlouhá část klotoidy bude použita pro napojení kruhové zatáčky o poloměru r = 450 m a kruhové zatáčky o poloměru r = 60 m.
Řešení: V bodech napojení musí mít klotoida i kruhová zatáčka stejnou křivost. Odtud vypočítáme křivočaré vzdálenosti L1, L2 bodů napojení od počátku při pohybu po klotoidě.
Délka použité části přechodnice bude rozdíl L = L2 - L1 =433,33 m.