Koordinatenvektoren
Parallelverschiebung (kurz: Schiebung)
Aufgabe 1
Das Dreieck ABC wird verschoben, der Bildpunkt von A ist A': a) Konstruiere das Bilddreieck A'B'C' und bestimme die Koordinaten von B' und C'. b) Welcher Zusammenhang zwischen den Koordinaten der Original- und der Bildpunkte ist zu erkennen?
c) Schreibe die Gleichungen von Aufgabe 1b übersichtlicher mit Hilfe von Koordinatenvektoren (Siehe: Rechnen mit Tupeln).
Aufgabe 2
Stelle die folgenden Vektoren a) durch je einen Punkt, b) durch je drei Pfeile mit den Anfangspunkten (2|2), (-1|3) und (3|-1) dar: . (Beschrifte die Punkte mit A, B, C und die Pfeile mit .)
Lösung
Aufgabe 3
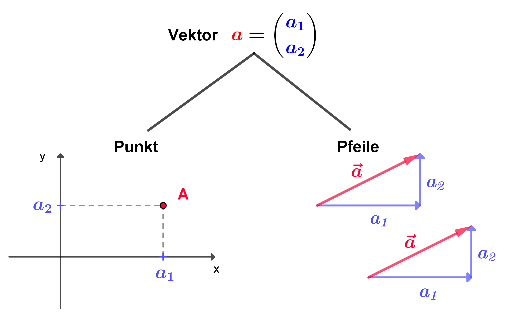
a) Die Koordinaten eines Punktes geben an, wie man vom Nullpunkt zu diesem Punkt gelangt. Ergänze: Die Koordinaten eines Pfeils geben an, wie man ... b) Welche geometrischen Beziehungen bestehen zwischen Pfeilen, die die gleichen Koordinaten haben?
Zusammenfassung
- Punkt,
- Menge von unendlich vielen Pfeilen, die parallel, gleich lang und gleich orientiert sind.