Дослідження на основі динамічних моделей окремих кривих
Епіциклоїда – це плоска крива, утворена фіксованою точкою кола, що котиться по зовнішній стороні іншого кола без ковзання. На відміну від циклоїди, вона не є трансцендентною. Вид
епіциклоїди та кількість її пелюстків залежить від співвідношення великого
нерухомого кола та кола, що котиться по ньому.
З окремими випадками епіциклоїди – кардіоїдою й нефроїдою – ми вже зустрічалися в описі побудов на основі функції Послідовність.
Задача на побудову 1. Створити модель генерації різних видів епіциклоїди, спираючись на її кінематичне визначення.
Навчальне дослідження 1. Опрацюйте
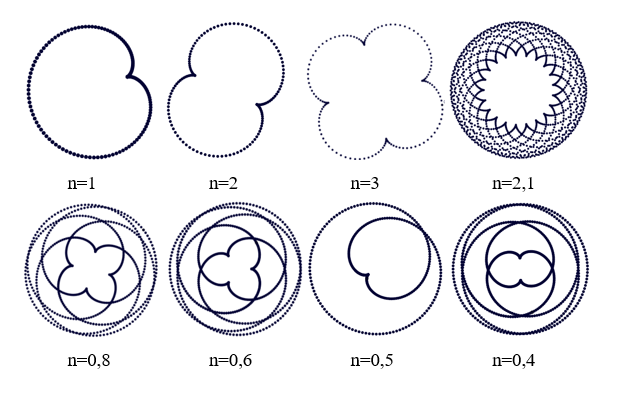
модель і переконайтесь, що кількість пелюсток епіциклоїди визначається
значенням n= R/r. Причому при цілому
n кількість пелюсток буде йому
відповідати.
Так, при n=1 епіциклоїда формуватиме кардіоїду,
при n=2 – нефроїду.
При нецілих значеннях,
наприклад, при n=2.1, кількість
пелюсток зростає до 21, при n=2.2 –
до 11.
При 0<n<1 крива епіциклоїди дещо змінює
притаманну їй форму: вона утворює кардіоїди з додатковими петлями, які,
накладаючись, створюють нові фігури.
При n=0 крива вироджується в коло.
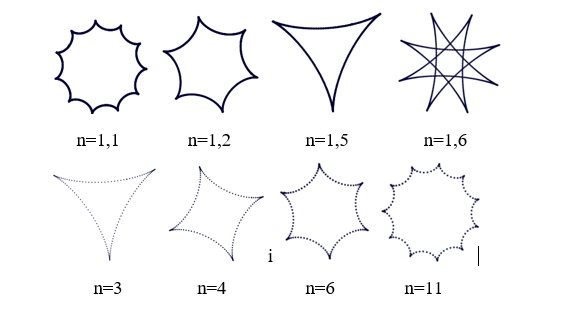
Гіпоциклоїда – це плоска
крива, яка утворюється точкою кола, що котиться по внутрішній стороні іншого
кола без ковзання. Вона багато в чому подібна епіциклоїді, побудову якої
описано вище. Динамічну модель гіпоціклоїди можна отримати, якщо внести в
оригінальну модель епіциклоїди такі зміни:

Навчальне дослідження 2. Спостерігайте за
роботою моделі і переконайтеся, що n
також є співвідношенням радіусів кіл R/r. Кількість пелюсток – каспів –
гіпоціклоїди також контролюється співвідношенням n. При цілих значеннях n
кількість каспів й n співпадатимуть.
При n=2 гіпоциклоїда буде вироджуватися в лінію діаметра більшої
окружності. Окремий випадок гіпоціклоїди з чотирма каспами (n=4) називається астроїдою.
При значеннях 1<n<2 гіпоциклоїда приймає форму, що
збігається з деякими випадками при n>1.
Так, форма кривої при n=1,5 і n=3 збігається, відрізняючись тільки за
розміром результуючої фігури, так само, як при n=1,2 і n= 6; n=1,5 і n=3.
При нецілих значеннях
n>2 кількість каспів зростає. Так, при n=3,5 маємо фігуру з 7 каспами, а при
n=3,9 – із 39 каспами.
При n=1 кривої не існує, так як рух моделі припиняється – обидва кола
прирівнюються в радіусі. При 0<n<1 крива вироджується в коло, при цьому
змінюється тільки швидкість руху точки.