1) Translation - Geometric Transformations (Unit 4)
Geogebra uses vectors to show translations. A vector is a quantity that has magnitude (size) and direction. It is represented by a directed line segment, a segment with an arrow at one end indicating the direction of movement that has a specific length.
Translate the triangle below using the vector u and then answer the following questions.Instructions:
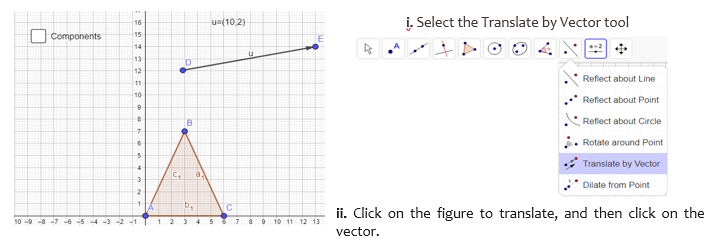
1) Complete the statements below. Write as 6 answers in order using a comma to separate them - To translate a shape you need to move the shape to a new _____________, - The triangle __________ is the image of the triangle ABC under a translation, - The directions of the the translation was given in terms of the __________ u, - The distance between the points: A and A’ is _________; B and B’ is _________ and C and C’ is ________
2) Describe the movement of the original triangle to its image using the previous statements. Indicate the units and direction.
3) To move a shape to a new position we can use one or more translations. Describe the movement of the original triangle to its image using two translations.
4) Click on the box: Vector_u Components and compare the two translations you used in the last question with the vector u. What can you conclude?
Observations: In the command Translate(t1, Vector_u*u), t1 is the shape we are going to translate, Vector_u is the name of the slider, * is the multiplication operation and u is the vector we will use to translate the shape.

6) Assume that the vector is v= (-10, 2) instead of u= (10, 2). a) Draw this vector v in Geogebra and translate the original triangle using it. b) Create a Slider to animate the motion of the triangle in the direction of the vector v. c) What does this translation with vector v differ from that performed with vector u?
7) Assume that the vector is p= (10, -2) instead of u= (10, 2). a) Draw this vector in Geogebra and translate the triangle using it. b) Create a Slider to animate the motion of the triangle in the direction of the vector p. c) What does this translation with vector p differ from that performed with vector u.
8) Assume that the vector is f= (-10,-2) instead of u= (10, 2). a) Draw this vector in Geogebra and translate the triangle using it b) Create a Slider to animate the motion of the triangle in the direction of the vector f. c) What does this translation with vector f differ from that performed with vector u?
9) Create a shape with more than three vertices and a vector z in the diagonal position. Then move the shape through this vector z. a) Describe the movement of your shape using one translation. b) Describe the movement of your shape using two translations.