Lage von Geraden im R3

Autor:
amutsch, Julia Lauss
Thema:
Geraden

Geraden im R2 und R3

Aufgabe 1: Begriffsklärung

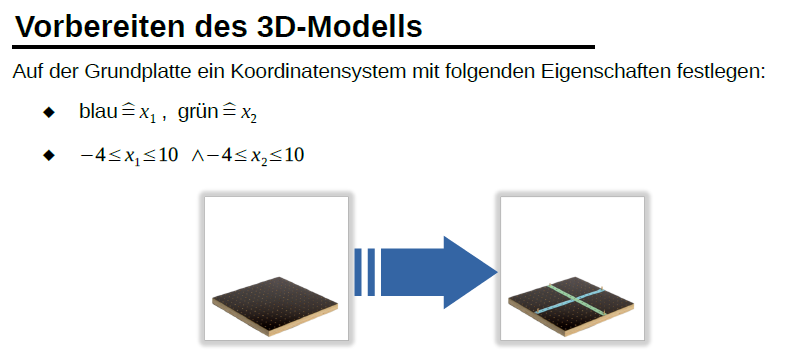
a) Die Abbildung oben rechts zeigt drei Geraden im dreidimensionalen Raum. Dieselben Geraden werden mit Blick "von oben" in der Abbildung links dargestellt (d.h. hier werden nur die x1- und dir x2-Achse dargestellt). Beschreiben Sie die Lage der Geraden im dreidimensionalen Raum (Abbildung oben rechts!) zueinander. Mehrere Antworten sind korrekt.

Wähle alle richtigen Antworten aus
  • A
  • B
  • C
  • D
  • E
  • F
  • G
  • H
  • I
Antwort überprüfen (3)

Notieren Sie die korrekten Ergebnisse auf Ihrem Arbeitsblatt. b) Welcher vierte Fall von Lagebeziehung zwischen zwei Geraden ist möglich? Geben Sie die Antwort unten ein. Wieso wurde er nicht abgebildet? Ergänzen Sie auf Ihrem Arbeitsblatt.

Antwort überprüfen
Darstellen von Geraden und rechnerische Ermittlung der Lagebeziehung In den folgenden vier Aufgaben sind jeweils zwei Geraden gegeben. Ihre Aufgabe ist es, diese Geraden im 3D-Modell jeweils paarweise darzustellen und das zugehörige LGS zu lösen. Bevor Sie loslegen, bereiten Sie das 3D-Modell wie folgt vor:
Image
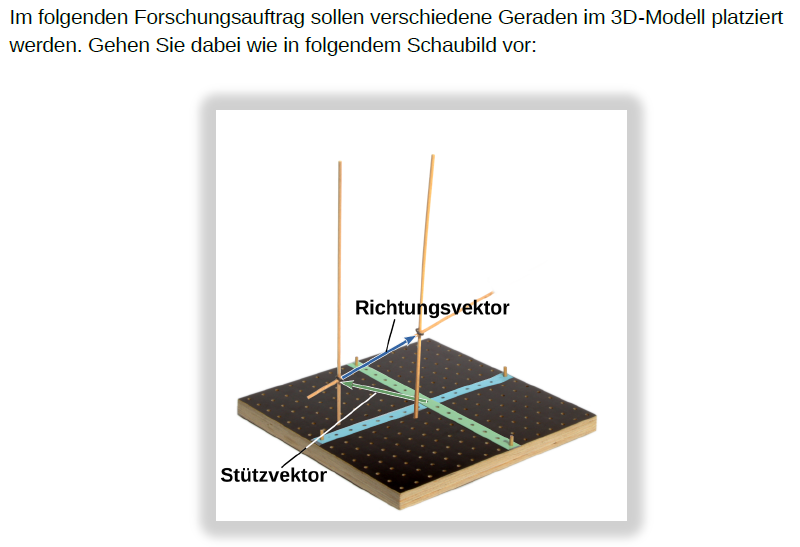
Hinweis: Mithilfe des Stützvektors kennzeichnen Sie den ersten Punkt der Geraden. Mithilfe der Geradengleichung ermitteln Sie einen weiteren Punkt auf der Geraden (z.B. Parameter =1) und können die Gerade somit festlegen.
Hinweis: Mithilfe des Stützvektors kennzeichnen Sie den ersten Punkt der Geraden. Mithilfe der Geradengleichung ermitteln Sie einen weiteren Punkt auf der Geraden (z.B. Parameter =1) und können die Gerade somit festlegen.

Aufgabe 2

Gegeben sind die Geraden und a) Platzieren Sie die Geraden im 3D-Modell. b) Beschreiben Sie in Worten die Lage der beiden Geraden zueinander:

Wähle alle richtigen Antworten aus
  • A
  • B
  • C
  • D
Antwort überprüfen (3)

c) Setzen Sie die beiden Geradengleichungen gleich und lösen Sie das zugehörige LGS. Wählen Sie das korrekte Ergebnis unten aus.

Wähle alle richtigen Antworten aus
  • A
  • B
  • C
  • D
  • E
Antwort überprüfen (3)
d) Welcher Zusammenhang besteht zwischen der Lage der Geraden und der Anzahl der Lösungen? Notieren Sie sich einen Merksatz auf Ihrem Arbeitsblatt. e) Entfernen Sie die Geraden wieder aus dem 3D-Modell.

Aufgabe 3

Gegeben sind die Geraden und a) Platzieren Sie die Geraden im 3D-Modell. b) Beschreiben Sie in Worten die Lage der beiden Geraden zueinander:

Wähle alle richtigen Antworten aus
  • A
  • B
  • C
  • D
Antwort überprüfen (3)

c) Setzen Sie die beiden Geradengleichungen gleich und lösen Sie das zugehörige LGS. Wählen Sie das korrekte Ergebnis unten aus.

Wähle alle richtigen Antworten aus
  • A
  • B
  • C
  • D
  • E
Antwort überprüfen (3)
d) Welcher Zusammenhang besteht zwischen der Lage der Geraden und der Anzahl der Lösungen? Notieren Sie sich einen Merksatz auf Ihrem Arbeitsblatt. e) Entfernen Sie die Geraden wieder aus dem 3D-Modell.

Aufgabe 4

Gegeben sind die Geraden und a) Platzieren Sie die Geraden im 3D-Modell. b) Beschreiben Sie in Worten die Lage der beiden Geraden zueinander:

Wähle alle richtigen Antworten aus
  • A
  • B
  • C
  • D
Antwort überprüfen (3)

c) Setzen Sie die beiden Geradengleichungen gleich und lösen Sie das zugehörige LGS. Wählen Sie das korrekte Ergebnis unten aus.

Wähle alle richtigen Antworten aus
  • A
  • B
  • C
  • D
  • E
Antwort überprüfen (3)
d) Welcher Zusammenhang besteht zwischen der Lage der Geraden und der Anzahl der Lösungen? Notieren Sie sich einen Merksatz auf Ihrem Arbeitsblatt. e) Entfernen Sie die Geraden wieder aus dem 3D-Modell.

Aufgabe 5

Gegeben sind die Geraden und a) Platzieren Sie die Geraden im 3D-Modell. b) Beschreiben Sie in Worten die Lage der beiden Geraden zueinander:

Wähle alle richtigen Antworten aus
  • A
  • B
  • C
  • D
Antwort überprüfen (3)

c) Setzen Sie die beiden Geradengleichungen gleich und lösen Sie das zugehörige LGS. Wählen Sie das korrekte Ergebnis unten aus.

Wähle alle richtigen Antworten aus
  • A
  • B
  • C
  • D
  • E
Antwort überprüfen (3)

Achtung!

d) Was fällt Ihnen beim Vergleich der Aufgaben 4 und 5 auf? Überlegen Sie, wie die beiden Fälle weiter voneinander abgegrenzt werden können (also: Woher weiß ich, welche Lagebeziehung die beiden Geraden zueinander haben, wenn ich kein Modell oder Schaubild habe?). Als Hilfestellung können vorne am Lehrerpult nochmals die Geraden von Aufgabe 4 im 3D-Modell eingesehen werden. e) Welcher Zusammenhang besteht zwischen der Lage der Geraden und der Anzahl der Lösungen? Notieren Sie sich einen Merksatz auf Ihrem Arbeitsblatt. f) Entfernen Sie die Geraden wieder aus dem 3D-Modell und verräumen Sie das gesamte Material wieder ordentlich in den Koffer.
Erarbeitung eines kürzeren Vorgehens

Aufgabe 6: Geradengleichungen

Betrachten Sie für jeden der obigen vier Fälle die Geradengleichungen paarweise genauer (z.B. g1 und g2). In welchen Fällen können Sie Besonderheiten feststellen? Ergänzen Sie die Erkenntnis bei den jeweiligen Fällen auf Ihrem Arbeitsblatt.

Aufgabe 7: Rechnerisches Vorgehen

Müssen wir stets LGS lösen, um die gegenseitige Lage von Geraden zu untersuchen? Mit der Erkenntnis aus Aufgabe 6 kann man das rechnerische Vorgehen nun etwas "abkürzen". Bearbeiten Sie die Learning App und notieren Sie die korrekten Ergebnisse auf Ihrem Arbeitsblatt.
Link

Link

https://learningapps.org/watch?v=pnnv1asen23

Für Schnelle:

Ermitteln Sie den Schnittpunkt der Geraden und aus Aufgabe 2. Geben Sie die Koordinaten von S in folgender Form unten ein: x1;x2;x3 (Strichpunkte ohne Leerzeichen, z.B. "3;4;5").

Antwort überprüfen

Für ganz Schnelle:

Bearbeiten Sie im Buch: S. 267 Nr. 7. Lösung:

Neue Materialien

Entdecke Materialien

Entdecke weitere Themen