Задачи для самостоятельного решения
Чтобы сделать раздаточный материал для каждого ученика, нажмите кнопку ASSIGN в правом верхнем углу. ↗
Указания школьникам
В каждой задаче надо построить подвижный чертёж, обнаружить элементы или величины, которые при движении чертежа остаются неизменными (длины отрезков, углы) или связаны между собой соотношением (равны, лежат на одной прямой и т. д.), и доказать это.
6.3. На стороне BC остроугольного треугольника ABC выбрана точка K. Точку K отразили относительно прямых AB и AC и получили точки L и S соответственно (см. рисунок). ↓↓
↑↑ Укажите две равные стороны четырёхугольника ASKL и два угла, которые не меняются при движении точки K по отрезку BC.
6.4. Пусть D — ортоцентр остроугольного треугольника ABC. а) Определите вид четырёхугольника с вершинами в серединах сторон четырёхугольника ABDC в зависимости от величины угла A. ↓↓
↑↑ б*) Найдите отношение двух его смежных сторон в зависимости от величины угла A.
Рисунок к задаче 6.5 ↓↓
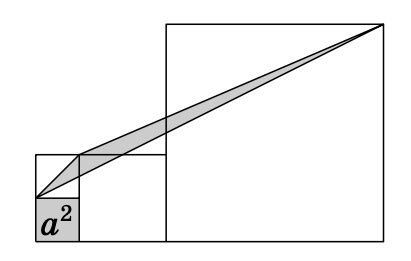
6.5. На рисунке ↑↑ площадь левого нижнего квадрата равна a². Размеры правого квадрата меняются. Можно ли найти площадь заштрихованного треугольника?
6.6. Известно, что если на сторонах квадрата наружу построить четыре квадрата, то их центры окажутся вершинами квадрата. На сторонах каких ещё выпуклых четырёхугольников можно построить наружу четыре квадрата, чтобы их центры были вершинами квадрата?
↑↑(Центр квадрата можно быстро построить, кликнув инструментом «Середина или центр» в два конца диагонали или просто во внутреннюю область квадрата.)
Рисунок к задаче 6.7 ↓↓
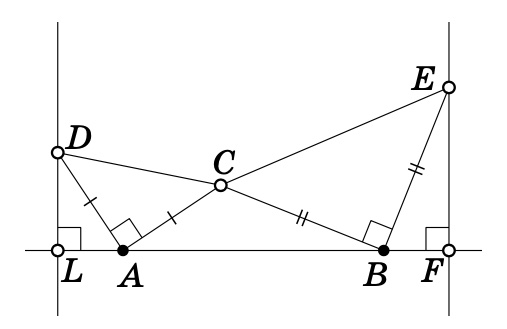
6.7. Даны фиксированная прямая AB и подвижная точка C вне её. Точки D и E — вершины прямоугольных равнобедренных треугольников CAD и CBE. Из точек D и E к прямой AB проведены перпендикуляры DL и EF (см. ↑↑ рисунок). ↓↓
↑↑ а) Укажите два равных отрезка.
б) Постройте множество отрезков DE и найдите их общее свойство.