Trabajo2: Sólidos platónicos y poliedro de Csás…
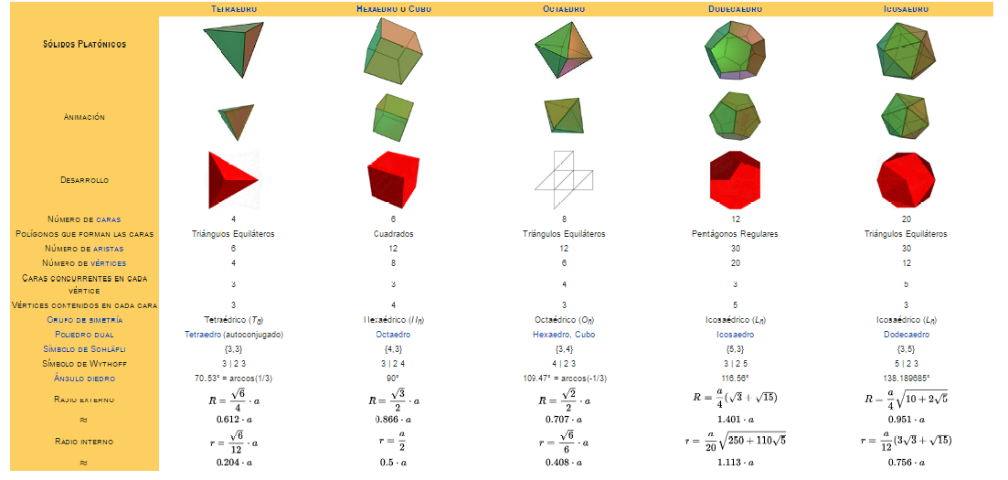
Existen sólo cinco poliedros que se puedan construir usando un polígono regular como cara y con el mismo número de caras en cada vértice. Los cinco Sólidos Platónicos son el tetraedro, cubo, octaedro, icosaedro y dodecaedro
Diagonales y su intersección
Poliedro de Császár
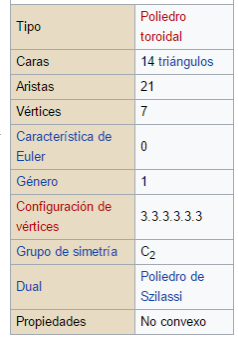
En geometría, el poliedro de Császár (ˈtʃaːsaːr) es un poliedro no convexo, topológicamente un toro, con 14 caras triangulares.
Este poliedro no tiene diagonales; cada par de vértices están conectados por una arista. Los 7 vértices y 21 aristas del poliedro forma el grafo completo sobre la superficie de un toro.
El tetraedro y el poliedro de Császár son los únicos poliedros conocidos que no tienen diagonales