Koordinaten LehrerInnenvortrag
Einführung - LehrerInnenvortrag + SchülerInnenfragen
Zu beginn wird ein Schachbrett ähnliches Spielfeld auf die Tafel gezeichnet und in dem Spielfeld wird eine Figur eingezeichnet. Nun wird den SchülerInnen die Frage gestellt:
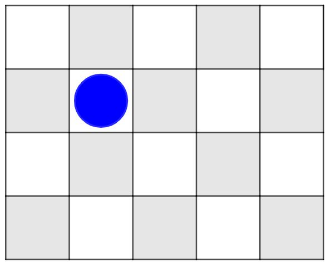
"Wie kann ich jemanden mitteilen, auf welches Feld ich die Figur gestellt habe?"
Die Schülerinnen und Schüler sollen sich nun Lösungen überlegen (alleine oder Partnerarbeit).
Die Lösungen werden dann gemeinsam betrachtet und es wird geschaut, ob man die Lösung verallgemeinern kann.
Beispiel: Felder durchnummerieren.
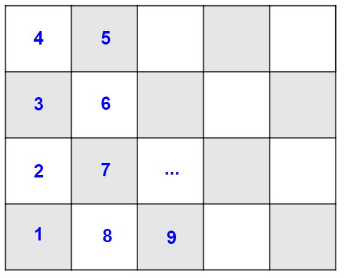
Hier würde die Figur auf Feld 6 stehen.
Funktioniert dies noch für sehr große Felder?
Wo fängt man an zu nummerieren?
Funktioniert das auch noch, wenn Figuren halbe Züge machen können?
Wenn SchülerInnen schon mal Schach oder Schiffeversenken gespielt haben, dann wird die Lösung mittels Buchstaben und Zahlen ein Koordinatensystem zu erstellen auch schnell kommen.
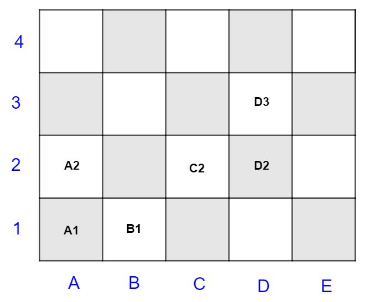
Hier steht die Figur auf Feld B3.
Wie geht man hier jedoch vor bei einem Feld, dass über 26 Felder breit ist?
Was passiert, wenn man einer Figur erlauben würde, halbe Züge zu machen?
Die naheliegende Lösung ist es die Buchstaben ebenfalls durch Zahlen zu ersetzen.
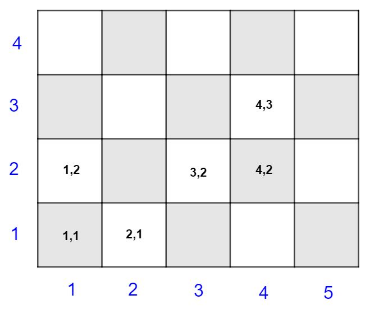
Ein weiteres Problem besteht jedoch. Wo ist jetzt genau die 1, oder die 2 definiert. Darum ist es stimmiger, wenn genau bei der 1 die Linie gezogen wird und nicht genau in der Mitte zwischen 1 und 2. Dies ist bereits vom Zahlenstrahl bekannt. Jetzt werden jedoch zwei Zahlenstrahlen im Rechten Winkel miteinander verbunden.
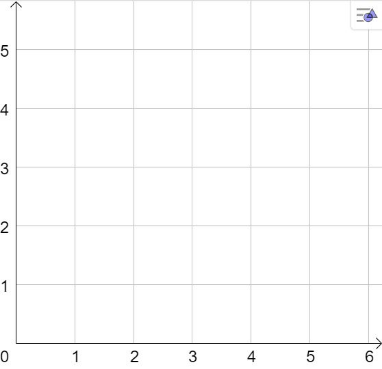
Hier lassen sich dann viel präzisere Aussagen treffen. So befindet sich unser Spielstein auf (1.5,2.5). Wenn man ihn jedoch leicht nach links rücken würde, so kann man dies ausdrücken, indem man sagt, der Spielstein befindet sich auf (1.4,2.5).
Dieses Spielfeld lässt sich unendlich groß erweitern.
Wie man damit umgeht, erfährt man im GeoGebrabook zu Koordinatensysteme.