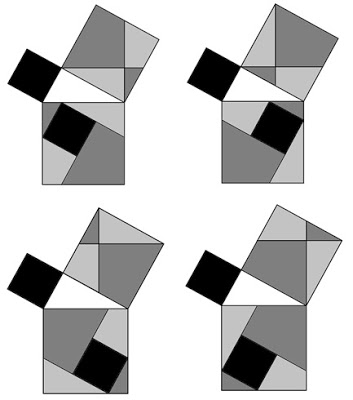
Teorema de Pitágoras (Perigal II)

Argomento:Geometria, Pitagora o teorema di Pitagora

NOTA INICIAL

Tomado de la Construcción 5.2 Teorema de Pitágoras de MANUAL PARA GEOGEBRA Guías para geometría dinámica, animaciones y deslizadores [Alexánder Borbón A.] Aplicación de la capacidad de GeoGebra en trabajar con transformaciones dinámicas, y uso de deslizadores.

Como vemos en la imagen siguiente, la conocida demostración del Teorema propuesta por Perigal muestra muchas posibles variantes... en esta actividad el Manual de Borbón propone construir una de ellas.

Construcción paso a paso

Abra un nuevo archivo en GeoGebra.
Oculte los ejes de coordenadas seleccionando en el menú Vista la herramienta Ejes.
Active la herramienta Segmento entre Dos Puntos y construya el segmento a entre los puntos A y B.
Active la herramienta Recta Perpendicular y construya la recta b que es perpendicular al segmento a y que pasa por el punto A.
Active la herramienta Nuevo Punto y construya el punto C en la recta b.
Active la herramienta Expone/Oculta Objeto para ocultar el segmento a y la recta b.
Active la herramienta Polígono y construya el triángulo ABC.
Active la herramienta Polígono Regular y construya tres cuadrados, uno en cada lado del triángulo; para ello marque dos vértices del triángulo e indique que el polígono tendrá cuatro lados (si el cuadrado queda dentro del triángulo deshaga con Ctrl-Z y ahora marque los vértices del triángulo en el orden contrario). Construya primero el cuadrado sobre la hipotenusa BC, de forma tal que quede el cuadrado BCED, luego sobre el lado CA de forma tal que quede el cuadrado CAGF y, por último, el cuadrado sobre el lado BA de tal forma que quede el cuadrado BAHI.
IMPORTANTE: Ahora mueva la ﬁgura hasta que el cuadrado CAGF sea más grande que el cuadrado BAHI (la demostración trabaja dividiendo el cuadrado recostado sobre el cateto mayor).
Active la herramienta Recta Paralela y construya la recta j que es paralela al segmento CE y que pasa por el punto G. También construya la recta k que es paralela al segmento ED por el punto F.
Active la herramienta Intersección entre Dos Objetos y construya el punto J que es la intersección de las dos rectas anteriores j y k. Calcule también la intersección K de la recta j con el lado del cuadrado CAGF y la intersección L de la recta k con el otro lado del cuadrado CAGF.
Active la herramienta Polígono y construya los polígonos CKJF, FJG, GJL y ALJK. Para cada uno de ellos haga clic derecho sobre él y elija la opción Configuración..., en la lengüeta de Color elija algún color distinto para cada uno.
Con la misma herramienta Polígono construya otro polígono ABIH y cámbiele el color.
Active la herramienta Deslizador y construya un deslizador llamado traslacion, este se debe deﬁnir de 0 a 1 con un incremento de 0.01. ~~Construya un segundo deslizador llamado iniciar con los valores que se dan por defecto~~.
Escriba en la línea de entrada: (a) M = J + traslacion ∗ (C − J) (b) N = J + traslacion ∗ (B − J) (c) O = J + traslacion ∗ (D − J) (d) P = J + traslacion ∗ (E − J)
Active la herramienta Compás y construya la circunferencia p con radio dado por los puntos F y J y cuyo centro es D (marque los tres puntos en ese orden). (Asegúrese que en realidad está marcando el punto D como centro del círculo, para ello se sugiere poner el deslizador traslacion en 0.5).
Active la herramienta Intersección entre Dos Objetos y construya el punto Q que es la intersección de la circunferencia p con el segmento DE.
Escriba en la línea de entrada: R = B + traslacion ∗ (Q − B)
Active la herramienta Vector entre Dos Puntos y construya el vector u del punto J al punto M, el vector v del punto J al punto N, el vector w del punto J al punto O, el vector z₁ del punto J al punto P y el vector m del punto B al punto R.
Active la herramienta Traslada Objeto por un Vector y marque en orden al polígono AKJL (marque el polígono en el centro, no los puntos) y el vector u, luego el polígono FCKJ con respecto al vector v, el polígono FJG con respecto al vector w, el polígono GJL con respecto al vector z₁ y el polígono ABIH con respecto al vector m.
Active la herramienta Elije y Mueve y mueva el deslizador traslacion para ver el efecto.
Active la herramienta Expone / Oculta Objeto para ocultar todos los objetos que ya no se necesiten: los vectores, los polígonos que no se mueven, etc. Active la herramienta Expone / Oculta Rótulo para ocultar todos los rótulos que no hagan falta.
Es posible activar la animación haciendo clic derecho sobre el deslizador y en el menú emergente active Animación Automática. Con esto inicia la animación; en la pantalla, en la esquina inferior izquierda aparecerá un pequeño botón, acciónelo para que pare la animación, y vuelva a apretarlo para que inicie de nuevo.
Modiﬁque el tamaño, el color y los estilos de su construcción.
Guarde el archivo.