Infinite Products
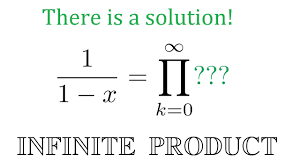
In calculus, an infinite product is a product of an infinite number of terms. It is analogous to an infinite series, where an infinite number of terms are added together. However, in an infinite product, an infinite number of terms are multiplied together.
Mathematically, an infinite product can be represented as:
P = an; when n = 1 to
where an represents the individual terms in the product, and n is the index that ranges from 1 to infinity.
Infinite products play a significant role in various areas of mathematics, including calculus and number theory. Some famous examples of infinite products include:
1. The Wallis Product: The Wallis product is used to calculate the value of . It is defined as:
; from n=1 to
By taking the limit of the product as n approaches infinity, we obtain the value of .
2. The Euler Product Formula: In number theory, the Euler product formula expresses the Riemann zeta function as an infinite product:
(s)=p
where the product is taken over all prime numbers p and (s) is the Riemann zeta function.
Infinite products can also be used to represent certain functions, series, and sequences. They often provide alternative representations of mathematical objects and can be used to derive interesting identities and relationships between different mathematical entities.
However, it's important to note that working with infinite products can be more challenging than dealing with finite products or infinite series. Convergence and divergence issues must be carefully considered when dealing with infinite products in calculus. Some infinite products may converge to a finite value, while others may diverge to infinity or approach zero. Proper techniques and tests, such as the ratio test or comparison test, are often employed to determine the convergence or divergence of infinite products.