Construcción utilizando el teorema de Pitágoras para representar números irracionales.
Ficha para la Actividad
• Nivel educativo al que va dirigida: Grado Octavo
• Objetivos de aprendizaje:
Identificar características de un numero Irracional dado
Representar los números Irracionales en GeoGebra.
Construir números Irracionales Positivos
• Descripción de la actividad:
Representación de números Irracionales, utilizando el programa de GeoGebra.
Mediante el siguiente concepto:
Los números irracionales se obtiene mediante la búsqueda de dos números naturales, a y b, tal que la suma de sus cuadrados de como resultado el
radicando.
Es decir que se cumpla el Teorema de Pitágoras donde:
Por lo tanto
Ejemplo
Busca el numero irracional de los números 2 y 3.
Lo primero que debemos hacer es remplazarlos en la formula donde
Se realizan las operaciones y se resuelve
Se obtiene el numero irracional
Ahora para convertirlo en numero decimal podemos usar la representación en GeoGebra.
Primer paso
Visita GeoGebra en línea:
https://www.geogebra.org/classic?lang=es
Segundo paso
Ve a la sección recta y haz clic en donde despliega seguidamente en la parte que dice segmento de Longitud dada
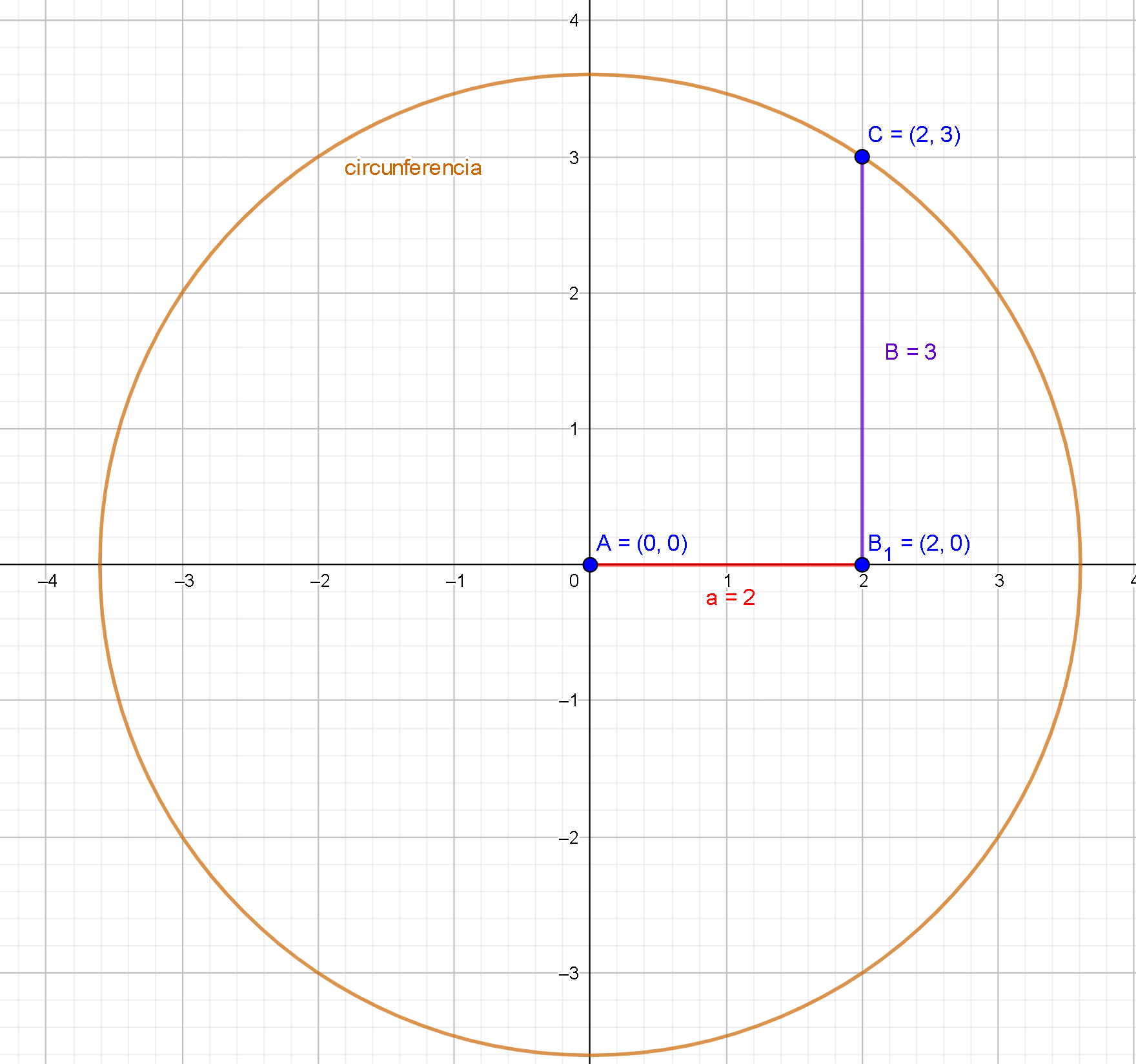
Debes seleccionar el punto de coordenadas (0,0) que será el punto A, y después darle la longitud que es 2.
Debes seleccionar el punto de coordenadas (0,0) que será el punto A, y después darle la longitud que es 2.Tercer paso.
El segmento te dará unto A y B
Debes realizar un punto, en la sección de arriba donde despliega, como se ve en la imagen, tres unidades arriba del punto B, es decir el punto C llevara las coordenadas (2,3), que lo ubicaras en el plano cartesiano:
Paso 4:
Quedan do de la siguiente manera
Paso 5:
En la función circunferencia como se ve la imagen le damos (centro y punto)
Una vez seleccionado seleccionamos el punto A que es el centro y el punto C, Que es lo que nos va a dar la intersección para dar solución al teorema de Pitágoras, que es la construcción del triángulo rectángulo.
Paso 6
Una vez realizada la circunferencia, vamos a la sección segmento y unimos el punto B y C en un segmento como se ve a continuación:
Paso 5:
En la función circunferencia como se ve la imagen le damos (centro y punto)
Una vez seleccionado seleccionamos el punto A que es el centro y el punto C, Que es lo que nos va a dar la intersección para dar solución al teorema de Pitágoras, que es la construcción del triángulo rectángulo.
Paso 6
Una vez realizada la circunferencia, vamos a la sección segmento y unimos el punto B y C en un segmento como se ve a continuación:
Paso 7
El número irracional, pedido queda determinado por la intersección entre la circunferencia (Punto C) y
el eje X (Punto A). Pera ello utiliza el botón intersección entre dos objetos.
Donde mediante la sección
insertar segmento podemos verificar al unir el punto A con el C, que es el
numero hallado donde
Como queda en la siguiente imagen:
Nota:
Cada vez que vayamos a insertar o a realizar una nueva acción, debemos darle en el botón mueve, ya que, si se coloca el cursor y se selecciona mas puntos, la ira colocando segmentos, circunferencia, puntos, de tal manera que no lo queremos, por lo tanto, es de vital importancia por cada paso darle en el cursor mueve que aparece en la parte lateral.
• Ficha para el alumno al que va dirigida esa actividad.
