6. Escala cromática
Esta actividad pertenece al libro de GeoGebra Música y Matemáticas.
La escala cromática
Pero, ¿qué sucede si elegimos la tonalidad Do menor? Es decir, empezar en Do pero siguiendo la pauta:
T h T T h T T
marcada por el modo menor. La respuesta fácil sería: “no se puede” y ya está. Pero esta respuesta no es satisfactoria, pues el motivo de la pregunta no es caprichoso. Podemos imaginar una melodía como una serie de instrucciones para subir o bajar los peldaños de la escala-escalera, al estilo “sube 1, después baja 3 y vuelve a subir 4”. Tal como están las cosas, si dos personas quieren cantar a la vez la misma melodía, solo se ajustarán sus voces si la diferencia de altura entre ambas es exactamente un número entero de octavas. Lo mismo pasará con los diferentes instrumentos. Por ejemplo, si una persona comienza a cantar en Do y sube un peldaño se encuentra en Re, mientras que otra que suba la misma altura comenzando en Mi se encontrará en... ¿en dónde? Según el gráfico, en un punto intermedio entre Fa y Sol, que no corresponde con ninguna nota de la escala diatónica. Hace falta añadir nuevas notas intermedias o, como se dice en Música, añadir color. Según el gráfico necesitamos notas entre cada dos separadas por un tono. Estas nuevas notas, cinco en total, reciben el nombre de alteraciones. Por ejemplo, podemos considerar la nueva nota entre Re y Mi como una alteración del Re (Re sostenido, Re#), aumentando un hemitono la frecuencia del Re, o una alteración del Mi (Mi bemol, Mi♭), disminuyendo un hemitono su frecuencia: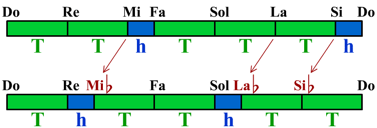
La escala así obtenida, con más color, se denomina escala cromática. Como ahora hay doce notas posibles que puedan elegirse como iniciales (tónicas), existirán 12 tonalidades diferentes en modo mayor y otras 12
tonalidades diferentes en modo menor.

Pero observamos que el problema está resuelto a medias. Hemos creado las cinco nuevas notas, en un proceso conocido como transposición, disminuyendo un hemitono las notas Re, Mi, Sol, La y Si, por lo que los intervalos rojos y azules coinciden en medida. Sin embargo, no son exactamente iguales a los intervalos verdes. El factor de incremento del hemitono es de 28/35, mientras que el de cada intervalo verde es de 37/211. Ambas fracciones no son equivalentes. Dicho de otra forma, Re sostenido (Re aumentado un hemitono) no coincide con Mi bemol (Mi disminuido un hemitono).
Para que ambas notas alteradas coincidiesen, es decir, para que las anteriores fracciones fuesen equivalentes, la fracción 312/219 =1,0136... debería ser exactamente la unidad. O, si se prefiere, 12 quintas (312/212) deberían coincidir con 7 octavas (27).
Este pequeño desajuste, conocido como “coma pitagórica”, ha sido motivo de preocupación e investigación durante siglos. El problema es que este desajuste, aunque ligero, es acumulativo, es decir, a medida que nos alejamos de la tónica, desplazándonos entre distintas octavas, el desajuste entre los intervalos se hace más evidente al oído.