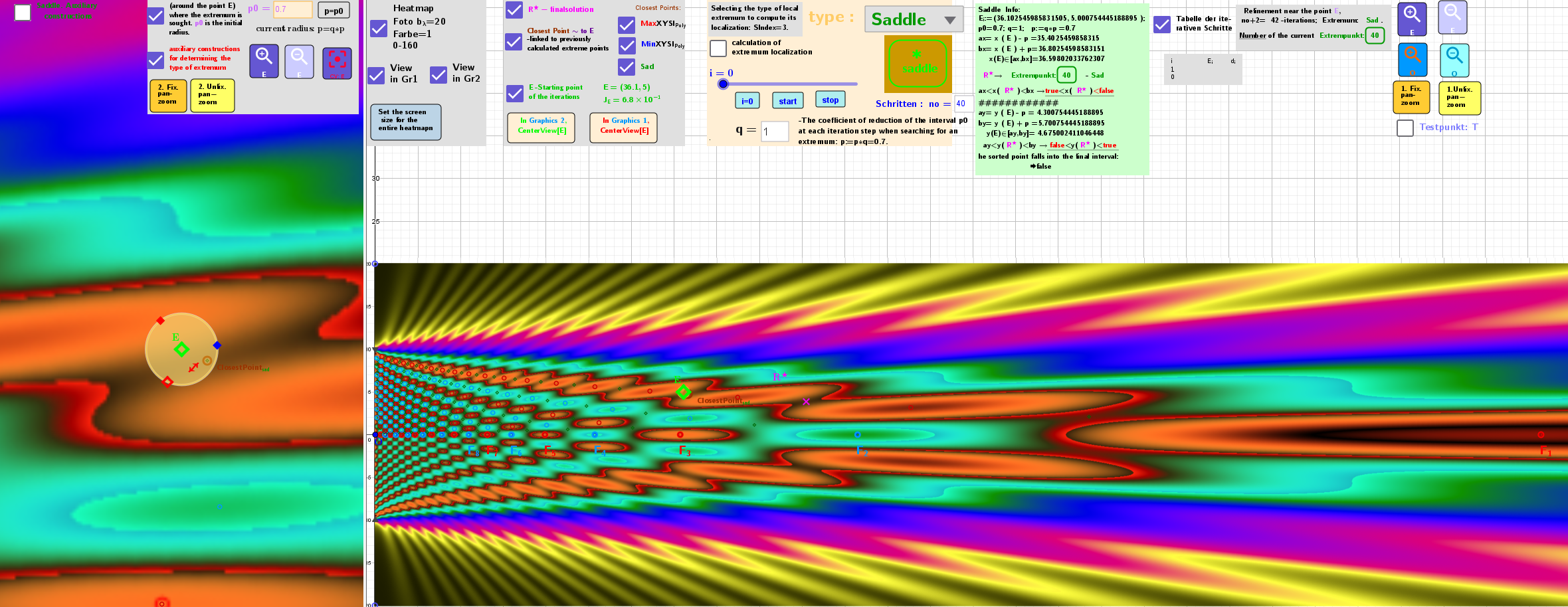
Images of the applet application of the coordinate descent-ascent algorithm for computing stationary points of a numerical function f(x,y) in the case of finding a saddle points

Szerző:Roman Chijner

Témák:Kalkulus

These Images were obtained using the applet.

The position of the starting point and the resulting point of the iterative process for finding the saddle point

The position of the starting point and the resulting point of the iterative process for finding the saddle point

[size=85][b][sup]*[/sup]Position of the starting point [color=#00ff00]E[/color] of the iterative process of finding the saddle point.

[b][b][size=85][color=#cc4125]Closest Point[/color], a point of a previously performed approximate solution.[/size][/b][/b][/b][/size] — ^*Position of the starting point E of the iterative process of finding the saddle point. Closest Point, a point of a previously performed approximate solution.

[b][sup][/sup][size=85][sup]*[/sup]Position of the resulting point [color=#ff00ff]R[sup]*[/sup][/color]of the iterative process of finding the saddle point.[/size][/b] — ^*Position of the resulting point R^*of the iterative process of finding the saddle point.

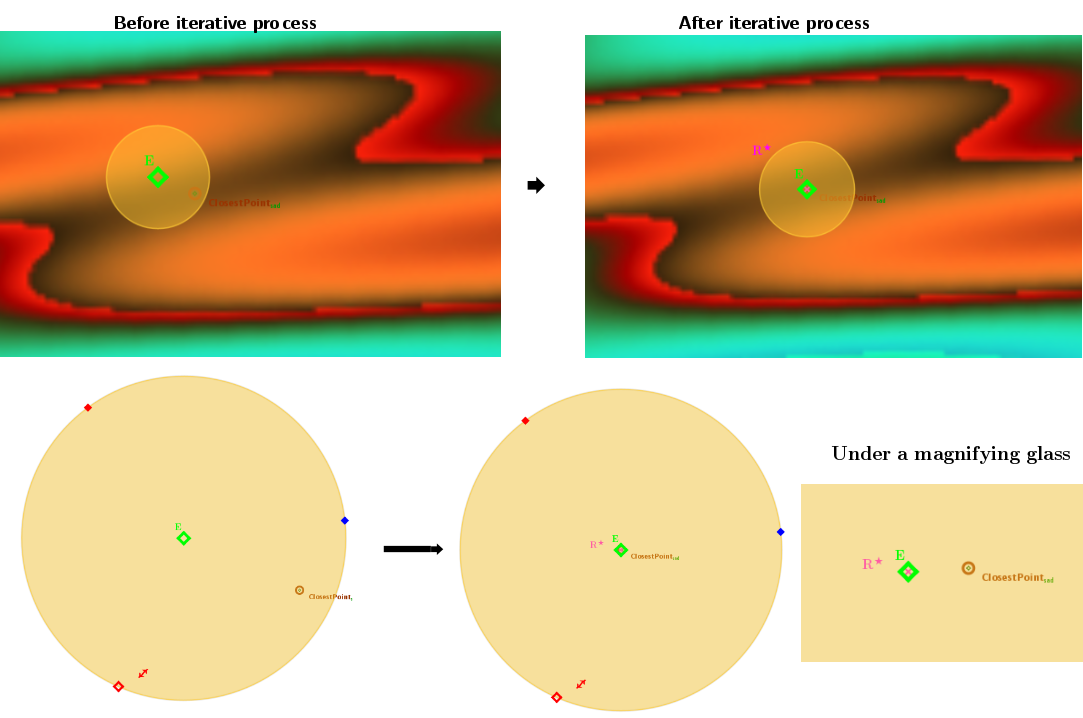
Before and After iterative process

Before and After iterative process — Closest Point, a point of a previously performed approximate solution.

Tables Before and After the Iterative Process

Tables Before and After the Iterative Process

Comparison of the diffraction field intensities before and after the iterative process with the Closest Point intensity for a point of a previously performed approximate.

Comparison of the diffraction field intensities before and after the iterative process with the Closest Point intensity for a point of a previously performed approximate. — R^* -The position of the resulting point of the iterative process for finding the saddle point.

Új anyagok

Anyagok felfedezése

Témák felfedezése