2.2 Definición Intuitiva de la Derivada
En análisis real y complejo, el concepto de límite es la clave de toque que formaliza la noción intuitiva de aproximación hacia un punto concreto de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a un determinado valor.
Para fórmulas, el límite se utiliza usualmente de forma abreviada mediante lim como en lim(an) = a o se representa mediante la flecha (→) como en an → a.
Límite de una Sucesión
La definición de límite matemático para el caso de una sucesión nos indica intuitivamente que los términos de la sucesión se aproximan arbitrariamente a un único número o punto  , si existe, para valores grandes de
, si existe, para valores grandes de  . Esta definición es muy parecida a la definición del cuando tiende a
. Esta definición es muy parecida a la definición del cuando tiende a  .
Formalmente, se dice que la sucesión
.
Formalmente, se dice que la sucesión  tiende hasta su límite
tiende hasta su límite  , o que converge o es convergente
, o que converge o es convergente  , y se denota como:
, y se denota como:
 Si y solo si para todo valor real ε>0 se puede encontrar un número natural
Si y solo si para todo valor real ε>0 se puede encontrar un número natural  tal que todos los términos de la sucesión, a partir de un cierto valor natural
tal que todos los términos de la sucesión, a partir de un cierto valor natural  mayor que
mayor que  , se acerquen a
, se acerquen a  cuando
cuando  crezca ilimitadamente. Escrito en un lenguaje formal, y de manera compacta:
crezca ilimitadamente. Escrito en un lenguaje formal, y de manera compacta:
 Este límite, si existe, se puede demostrar que es único. Si los términos de la sucesión no convergen a ningún punto específico, entonces se dice que la sucesión es divergente.
Límite de una Función
Se dice que el límite de la función f(x) cuando x tiende a c es L , y se escribe:
Este límite, si existe, se puede demostrar que es único. Si los términos de la sucesión no convergen a ningún punto específico, entonces se dice que la sucesión es divergente.
Límite de una Función
Se dice que el límite de la función f(x) cuando x tiende a c es L , y se escribe:
 Si se puede encontrar para cada ocasión un x suficientemente cerca de c tal que el valor de f(x) sea tan próximo a L como se desee.
Si se puede encontrar para cada ocasión un x suficientemente cerca de c tal que el valor de f(x) sea tan próximo a L como se desee.
 Esta definición es equivalente al límite de una sucesión, una función es continua si:
Esta definición es equivalente al límite de una sucesión, una función es continua si:

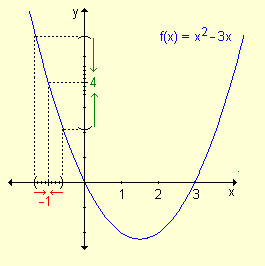 Recta Secante
Es una recta que corta a una curva en 2 puntos. Conforme estos puntos se acercan y su distancia se reduce a cero, la recta adquiere el nombre de recta tangente. Dados los puntos de intersección A y B puede calcularse la ecuación de la recta secante.
Cuando aproximamos a+h a a obtenemos la recta secante, en azul. En este caso, su pendiente será m tangente = tan α = lim h → 0 f a + h - f a h = f ' a . En ocasiones se define la recta tangente como aquella que corta a la función en un único punto.
Recta Secante
Es una recta que corta a una curva en 2 puntos. Conforme estos puntos se acercan y su distancia se reduce a cero, la recta adquiere el nombre de recta tangente. Dados los puntos de intersección A y B puede calcularse la ecuación de la recta secante.
Cuando aproximamos a+h a a obtenemos la recta secante, en azul. En este caso, su pendiente será m tangente = tan α = lim h → 0 f a + h - f a h = f ' a . En ocasiones se define la recta tangente como aquella que corta a la función en un único punto.
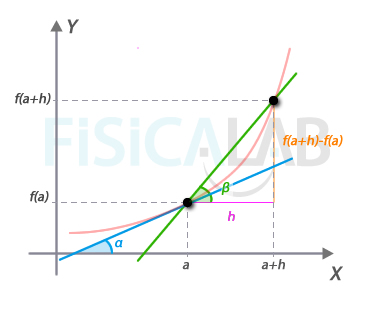 Recta Tangente
La tangente a una curva en un punto P es una recta que toca a la curva solo en dicho punto, llamado punto de tangencia. Se puede decir que la tangente forma un ángulo nulo con la curva en la vecindad de dicho punto.
Recta Tangente
La tangente a una curva en un punto P es una recta que toca a la curva solo en dicho punto, llamado punto de tangencia. Se puede decir que la tangente forma un ángulo nulo con la curva en la vecindad de dicho punto.  Link del vídeo:
https://www.youtube.com/watch?v=lf6k_zCqo2M
https://www.youtube.com/watch?v=RdLtaXRO_Ik
Link del vídeo:
https://www.youtube.com/watch?v=lf6k_zCqo2M
https://www.youtube.com/watch?v=RdLtaXRO_Ik
 , si existe, para valores grandes de
, si existe, para valores grandes de  . Esta definición es muy parecida a la definición del cuando tiende a
. Esta definición es muy parecida a la definición del cuando tiende a  .
Formalmente, se dice que la sucesión
.
Formalmente, se dice que la sucesión  tiende hasta su límite
tiende hasta su límite  , o que converge o es convergente
, o que converge o es convergente  , y se denota como:
, y se denota como:
 Si y solo si para todo valor real ε>0 se puede encontrar un número natural
Si y solo si para todo valor real ε>0 se puede encontrar un número natural  tal que todos los términos de la sucesión, a partir de un cierto valor natural
tal que todos los términos de la sucesión, a partir de un cierto valor natural  mayor que
mayor que  , se acerquen a
, se acerquen a  cuando
cuando  crezca ilimitadamente. Escrito en un lenguaje formal, y de manera compacta:
crezca ilimitadamente. Escrito en un lenguaje formal, y de manera compacta:
 Este límite, si existe, se puede demostrar que es único. Si los términos de la sucesión no convergen a ningún punto específico, entonces se dice que la sucesión es divergente.
Límite de una Función
Se dice que el límite de la función f(x) cuando x tiende a c es L , y se escribe:
Este límite, si existe, se puede demostrar que es único. Si los términos de la sucesión no convergen a ningún punto específico, entonces se dice que la sucesión es divergente.
Límite de una Función
Se dice que el límite de la función f(x) cuando x tiende a c es L , y se escribe:
 Si se puede encontrar para cada ocasión un x suficientemente cerca de c tal que el valor de f(x) sea tan próximo a L como se desee.
Si se puede encontrar para cada ocasión un x suficientemente cerca de c tal que el valor de f(x) sea tan próximo a L como se desee.
 Esta definición es equivalente al límite de una sucesión, una función es continua si:
Esta definición es equivalente al límite de una sucesión, una función es continua si:

 Recta Secante
Es una recta que corta a una curva en 2 puntos. Conforme estos puntos se acercan y su distancia se reduce a cero, la recta adquiere el nombre de recta tangente. Dados los puntos de intersección A y B puede calcularse la ecuación de la recta secante.
Cuando aproximamos a+h a a obtenemos la recta secante, en azul. En este caso, su pendiente será m tangente = tan α = lim h → 0 f a + h - f a h = f ' a . En ocasiones se define la recta tangente como aquella que corta a la función en un único punto.
Recta Secante
Es una recta que corta a una curva en 2 puntos. Conforme estos puntos se acercan y su distancia se reduce a cero, la recta adquiere el nombre de recta tangente. Dados los puntos de intersección A y B puede calcularse la ecuación de la recta secante.
Cuando aproximamos a+h a a obtenemos la recta secante, en azul. En este caso, su pendiente será m tangente = tan α = lim h → 0 f a + h - f a h = f ' a . En ocasiones se define la recta tangente como aquella que corta a la función en un único punto.
 Recta Tangente
La tangente a una curva en un punto P es una recta que toca a la curva solo en dicho punto, llamado punto de tangencia. Se puede decir que la tangente forma un ángulo nulo con la curva en la vecindad de dicho punto.
Recta Tangente
La tangente a una curva en un punto P es una recta que toca a la curva solo en dicho punto, llamado punto de tangencia. Se puede decir que la tangente forma un ángulo nulo con la curva en la vecindad de dicho punto.