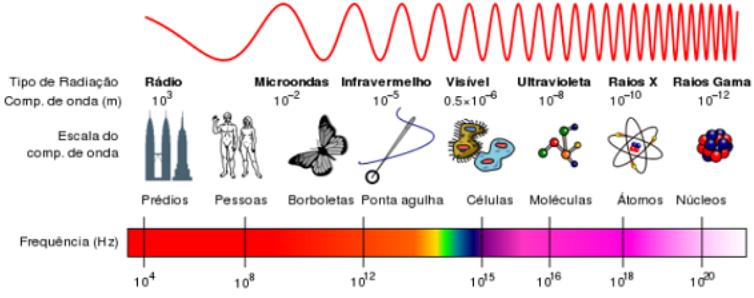
Onda harmônica
As soluções das equações (8) e (9) expressam os campos vetoriais, elétrico e magnético, propagando-se no vácuo e variando no tempo. Como no vácuo não há dispersão, a perturbação não é alterada durante a propagação, isto é, o campo apresenta em necessariamente a mesma configuração, com exceção da intensidade, que em , tendo em vista ser um movimento retilíneo e uniforme: a luz viaja em linha reta com velocidade escalar . Destarte, as soluções são necessariamente:
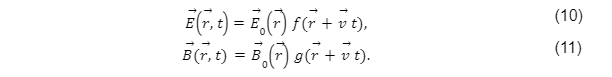
Sendo o primeiro fator expressão referente à intensidade e orientação vetorial dos campos, enquanto o segundo à fase da perturbação.
Um caso particular muito interessante na Ondulatória é o qual as perturbações são periódicas, nessas os fatores escalares das soluções das (10) e (11) consistem da função seno ou cosseno, e a onda é dita harmônica:
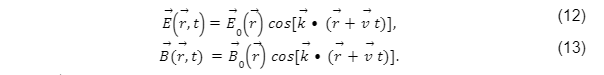
Sendo o dito vetor de onda, o qual apresenta a direção da propagação da onda e tem magnitude de , sendo o comprimento de onda, isto é, o período espacial.
Ademais, como nesse caso a perturbação periódica, pode-se obter a velocidade de propagação ao dividir o período espacial, , pelo temporal, , e, consequentemente, a relação de dispersão:
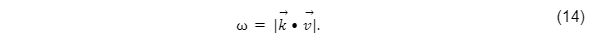
Sendo a frequência angular temporal da onda e, o também conhecido como número de onda, a frequência angular espacial.
Destarte, mediante a relação de dispersão, as soluções harmônicas dos campos apresentam frequência ,
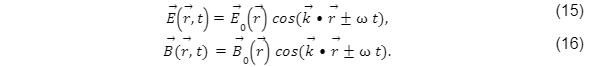
Sendo que cada frequência possível remete a uma cor, ou seja, a onda eletromagnética harmônica é monocromática. Com exceção da luz branca, que é a superposição de diversas ondas harmônicas/monocromáticas. Abaixo ilustra-se o espectro eletromagnético.