3. Sequência de Sierpinski
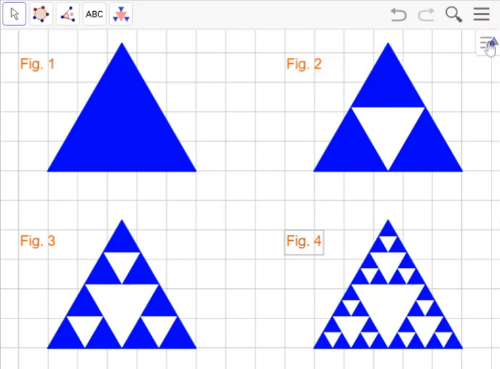
O Triângulo de Sierpinski leva este nome em homenagem a Waclaw Sierpinski, matemático polonês que o definiu. É obtido por meio de um processo iterativo de divisão de um triângulo equilátero em quatro triângulos semelhantes.
Objetivo: Explorar em sala de aula, o conceito de sequências, promovendo a pesquisa de padrões e regularidades e formulando generalizações.
Questão 1
Suponha que o triângulo equilátero mostrado na figura 1 tenha área unitária (Área = 1). Na figura 2, este triângulo é dividido em 4 triângulos equiláteros, dos quais são pintados 3. Qual o valor da área pintada na figura 2? Por quê?
2) Agora, para construir a figura 3, cada triângulo azul é dividido em 4 triângulos equiláteros, dos quais 3 são pintados como mostrado no vídeo:
Questão 2
Na figura 1 é mostrado um triângulo equilátero de área unitária. Qual seria o valor da área pintada na figura 3? Por quê?
3) Tudo bem? Para construir a figura 4, cada triângulo azul é dividido em 4 triângulos equiláteros, dos quais 3 são pintados como mostrado no vídeo:
Questão 3
Na figura 1 é mostrado um triângulo equilátero de área unitária. Qual seria o valor da área pintada na figura 4? Por quê?
Preencha a tabela:
Questão 4
Finalmente, podemos calcular a área da figura 5 sem precisar desenhá-la? Você observa alguma sequência no valor das áreas?