INTRODUCCIÓN A LA ELIPSE
- Autor:
- Oscar Corzo
- Tema:
- Elipse
Ecuaciones
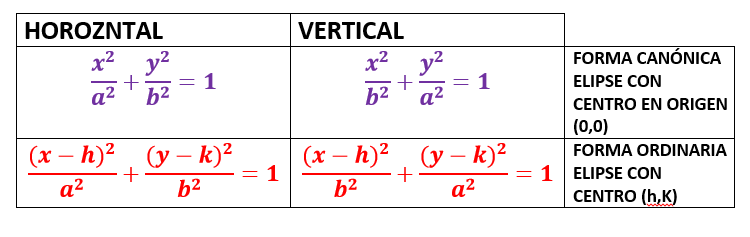
Ejemplo Ecuación de la Elipse con Centro en el Origen 0,0)
Ejemplo Ecuación de la Elipse con Centro (h,k)
Ecuación dados el centro y sus focos
Gráfica y Elementos de la elipse
La elipse es el conjunto de puntos cuya suma de distancias a dos puntos fijos llamados focos es igual a una constante, su figura se caracteriza por tener dos ejes: un eje mayor y un eje menor, los focos se localizan sobre el eje mayor. Consideremos una elipse cuyo centro es , distancia focal , eje mayor horizontal , se genera un eje menor mediante la siguiente relación: . La ecuación cartesiana de la elipse vendrá dada por: . También se define la excentricidad como la relación entre la distancia focal y el eje mayor: o la relación entre la distancia de cualquier punto de la elipse a un foco y la distancia del punto a una recta fija llamada recta directriz , en la elipse la excentricidad siempre es menor que 1, y cuanto más se acerque a cero más se parece a una circunferencia.