Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Função do Segundo Grau

Author:Inaya Faria Nomura
Uma função do 2º grau, ou função quadrática é um tipo específico de função. Dada pela lei de formação f(t) = at² +bt +c. Aqui, t é a variável (número que você pode escolher e trocar), e a, b, e c são os coeficientes.
  • a não pode ser 0.
  • t² significa que você multiplica o número escolhido por ele mesmo (txt).
  • bt significa que você multiplica o número escolhido por b.
  • c é apenas um número constante (valor fixo).

Vamos identificar os coeficientes:

f(x) = 2x²+3x + 1

Check my answer

g(t) = -t² + 4

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

h(x) = x² – x

Check my answer

Marque mais de uma alternativa z(s)=s²

Select all that apply
  • A
  • B
  • C
  • D
  • E
  • F
Check my answer (3)
A função do segundo grau é chamada assim porque a variável x é elevado ao quadrado (x2). A presença dessa potência de 2 faz com que o gráfico da função seja uma curva chamada parábola. A função do primeiro grau ou função afim, com a variável x é elevado a um (x1), é uma reta.

Gráfico da função do primeiro grau ou função afim, com f(x)=x

Gráfico da função do segundo grau ou função quadrática, com f(x)=x²

Gráfico da função do terceiro grau ou função cúbica, com f(x)=x³

Coeficientes Os coeficientes a, b, e c afetam a forma e a posição da parábola no plano cartesiano. Em particular:

Mova o controle deslizante a para 3, depois para 0 e posteriormente para -3

Com suas palavras o que você percebeu, após mover com o controle deslizante? O que ocorre com o gráfico nesses três valores?

Mova o controle deslizante b para 3, depois para 0 e posteriormente para -3

Com suas palavras o que você percebeu, após mover com o controle deslizante? O que ocorre com o gráfico nesses três valores?

Mova o controle deslizante c para 3, depois para 0 e posteriormente para -3

Com suas palavras o que você percebeu, após mover com o controle deslizante? O que ocorre com o gráfico nesses três valores?

Substituição do valor da variável Para encontrar o valor numérico de qualquer função, conhecendo a sua lei de formação, basta realizarmos a substituição do valor da variável para encontrar a imagem. Se quisermos descobrir os pontos podemos fazer essa substituição por valores de x, para encontrar a Imagem f(x). Por exemplo, temos a função f(x)=x²+2x+2. Para x=0, temos f(0)=0²+2.0+2=0+0+2=2. Logo, obtemos o ponto (0,2), coordenadas de x (horizontal) no 0 e y(vertical) no 2. Para x=1, temos f(1)=1²+2.1+2=1+2+2=5. Logo, obtemos o ponto (1,5), coordenadas de x (horizontal) no 1 e y(vertical) no 5.

Gráfico da função do segundo grau ou função quadrática, com f(x)=x². Com ponto A=(0,2) e ponto B=(1,5)

Dada a função f(x)=x²+2x+2. Para x=-1, temos qual valor para f(-1)? Também escreva qual será o ponto (?,?).

Check my answer

Gráfico da função do segundo grau ou função quadrática, com f(x)=x². Com ponto A=(0,2) e ponto B=(1,5). Agora escreva o ponto C de acordo com o que você descobriu na pergunta anterior.

OBS.: Se você quiser apagar um ponto, vá com o botão direito do mouse, depois em apagar.

Ache as raízes da seguinte função f(x)=x² +2x + 1

Check my answer
Raízes da função de 2º grau Para encontrar as raízes da função quadrática, conhecidas também como zero da função é necessário utilizar um método, podendo ser a fórmula de Bhaskara e a soma e produto. As raízes de uma função quadrática são os valores de x que fazem com que f(x) = 0. Sendo assim, para encontrar as raízes de uma equação do 2º grau, faremos ax² + bx + c = 0.

Fórmula de Bhaskara

Fórmula de Bhaskara

Soma e Produto

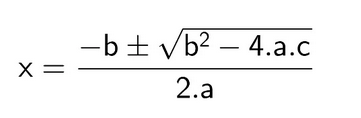
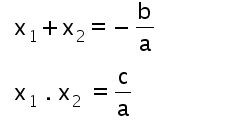
Soma e Produto

Ache as raízes da seguinte função f(x) = x² +2x – 3.

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)
Vértice da parábola O vértice da parábola é o ponto de mínimo ou de máximo do gráfico. Para encontrar o valor de x e y no vértice, utilizamos uma fórmula específica. Vale ressaltar que o vértice é um ponto V, logo ele possui coordenadas, representadas por xv e yv. Para calcular o valor de V (xv, yv), utilizamos as fórmulas:
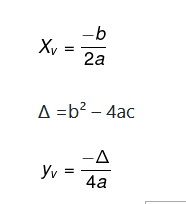
Image

Encontre o vértice da parábola f(x) = –x² +4x – 3.

Encontre o vértice da parábola f(x) = x² +4x +4.

New Resources

Discover Resources

Discover Topics