Ecuaciones de primer grado resueltas
Recordad que si sumando los monomios con igual parte literal obtenemos una
- igualdad imposible (como 1 = 2), la ecuación no tiene solución.
- igualdad que siempre se cumple (como 1 = 1), cualquier valor es solución de la ecuación, es decir, la solución es todos los reales.
Ecuación 1
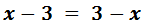
Pasamos las x's a un lado de la igualdad (izquierda) y los números al otro lado (derecha):
En la derecha, la x está restando. Pasa a la izquierda sumando:
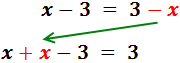
Sumamos los monomios con x’s:
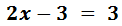
En la izquierda, el -3 está restando. Pasa a la derecha sumando:
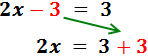
Sumamos los monomios de la derecha:
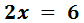
El coeficiente de la x es 2. Este número está multiplicando a x, así que pasa al otro lado dividiendo:
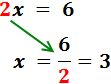
Por tanto, la solución de la ecuación es x = 3.Ecuación 2
Recordamos que los paréntesis sirven para agrupar elementos, para simplificar o para evitar ambigüedades.
El signo negativo de delante del paréntesis indica que los monomios que contiene tienen que cambiar de signo:
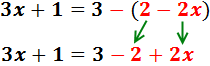Sumamos 3 y -2 en el lado derecho:
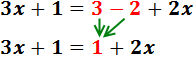Pasamos los monomios con x’s a la izquierda y los números a la derecha:
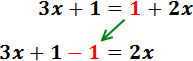Sumamos 1 y -1. Como el resultado es 0, no lo escribimos:
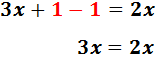Pasamos 2x a la izquierda restando y sumamos los monomios:
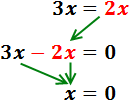Luego la solución de la ecuación es x = 0.
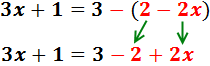Sumamos 3 y -2 en el lado derecho:
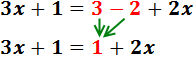Pasamos los monomios con x’s a la izquierda y los números a la derecha:
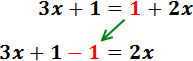Sumamos 1 y -1. Como el resultado es 0, no lo escribimos:
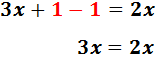Pasamos 2x a la izquierda restando y sumamos los monomios:
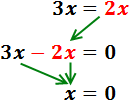Luego la solución de la ecuación es x = 0.
Problema 1
Encontrar el número que cumple que la suma de su doble y de su triple es igual a 100.
Si x es el número que buscamos, su doble es 2⋅x y su triple es 3⋅x. La suma de los dos últimos debe ser 100:
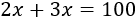Resolvemos la ecuación:
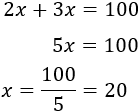El número buscado es 20.
En efecto, el doble de 20 es 40, su triple es 60 y ambos números suman 100.
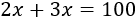Resolvemos la ecuación:
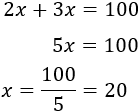El número buscado es 20.
En efecto, el doble de 20 es 40, su triple es 60 y ambos números suman 100.Problema 2
Si Ana es 12 años menor que Eva y dentro de 7 años la edad de Eva es el doble que la edad de Ana, ¿qué edad tiene Eva?
Supongamos que x es la edad de Ana. Como Eva tiene 12 años más que Ana, su edad es x+12.
Dentro de 7 años, Ana tendrá la edad actual más 7, es decir, tendrá x+7. Del mismo modo, Eva tendrá (x+12)+7=x+19. Además, el doble de la edad de Ana será 2⋅(x+7).
Debemos resolver la ecuación
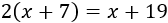Resolvemos la ecuación:
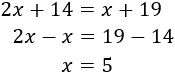Por tanto, la edad actual de Ana es 5 y la de Eva es 17. Dentro de 7 años, Ana tendrá 12 y Eva tendrá 24 (el doble que Ana).
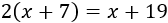Resolvemos la ecuación:
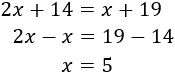Por tanto, la edad actual de Ana es 5 y la de Eva es 17. Dentro de 7 años, Ana tendrá 12 y Eva tendrá 24 (el doble que Ana).
Más ecuaciones resueltas:
Ecuaciones de primer grado:
- Nivel 1: Primeras ecuaciones (nivel 1)
- Nivel 2: Número de soluciones (nivel 2)
- Nivel 3: Ecuaciones con paréntesis (nivel 3)
- Nivel 4: Ecuaciones con fracciones (nivel 4)
- Nivel 5: Ecuaciones con fracciones y con paréntesis (nivel 5)
- Nivel 6: Problemas de ecuaciones (nivel 6)
- Nivel 1: Introducción a las ecuaciones cuadráticas
- Nivel 2: Discriminante y número de soluciones
- Nivel 3: Resolver ecuaciones incompletas
- Nivel 4: Resolver ecuaciones completas
- Nivel 5: Soluciones complejas