Herhalingsoefeningen V trimester 1 schooljaar 2526
Vraag 1
Welke transformatie verandert de grafiek van in de grafiek van
Vraag 2
Zij -2. De periode en bereik van f zijn respectievelijk
Vraag 3
De inverse van de functie is
Vraag 4
De grafiek van heeft als asymptoten
Vraag 5
als een factor is van , met , dan is a gelijk aan
Vraag 6
De som van de eerste vier positieve oplossingen van is
Vraag 7
Een reële veelterm van de vierde graad heeft -1 als nulwaarde met multipliciteit 2. Welke waarden hebben de coëfficiënten ?
Vraag 8
Het domein van is:
Vraag 9
Los op :
Vraag 10
Bepaal de mogelijke waarde(n) van de parameter k zodat de vergelijking twee oplossingen heeft.
Vraag 11
De uitdrukking kan herschreven worden tot
Vraag 12
Als dan is
Vraag 13
De functie f(x) voldoet aan f(f(x))=x, een mogelijk functievoorschrift voor f(x) is
Vraag 14
De algemene oplossing van wordt gegeven door (met )
Vraag 15
De functie heeft een inverse functie. Bepaal de maximale waarde van a
Vraag 16
Een functie f heeft de volgende twee eigenschappen voor elke waarde van : en: . Een mogelijk functievoorschrift is
Vraag 17
De grafiek van de functie heeft
Vraag 18
Zij met k een parameter. Als dan heeft de parameter k de waarde:
Vraag 19
Als met en dan is gelijk aan
Vraag 20
Neem aan dat a,b>0. Waaraan is de volgende uitdrukking gelijk?
vraag 21
Bepaal het functievoorschrift waarvan hier de grafiek gegeven is. Geef ook de transformaties die nodig zijn vertrekkende van de basisgrafiek.
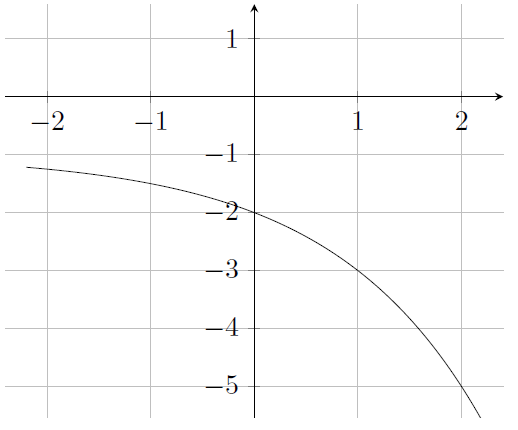 .
.
Vraag 22
gegeven . Bereken x
Vraag 23
De volgende vijf uitdrukkingen nemen verschillende waarden aan als je k vervangt door alle mogelijke gehele getallen. Welke van de vijf zal het minste aantal verschillende waarden aannemen?
Vraag 24
is gelijk aan ...
Vraag 25
Bij deling van de veelterm a x³ - 2 x² + bx - 4 door x -2 is de rest 2. Bij deling van diezelfde veelterm door x -3 is de rest 14. Bepaal de rest bij deling van deze veelterm door x - 1 .
Vraag 26
Als een egelpopulatie elk jaar met 10% afneemt, hoeveel procent van de oorspronkelijke populatie blijft er dan nog over na 5 jaar?
Vraag 27
als en dan is