6.1 (II) Entdecke allgemeine Potenzfunktionen
In der allgemeinen Form sieht eine Potenzfunktion wie folgt aus:
mit aber und.
(Der Parameter a ist Koeffizient, der Parameter n ist Exponent.)
Den Einfluss des Parameters a auf den Graphen kannst du mit dem folgendem Applet untersuchen.
Verschiebe dazu den Schieberegler und beantworte mit Hilfe deiner Beobachtungen die Fragen.
Der Parameter a ...
Für gerade n:
Umso größer der Parameter a, ...
Diese Beobachtung gilt auch für ungerade n, allerdings passt hier der Begriff "Öffnung" nicht so recht.
Hat das a ein negatives Vorzeichen, so ...
Das folgende Diagramm stellt zum einen den Graphen von (gestrichelt) dar. Der andere Graph gehört zum Funktionsterm . Gib das Intervall an, in dem a liegen muss.
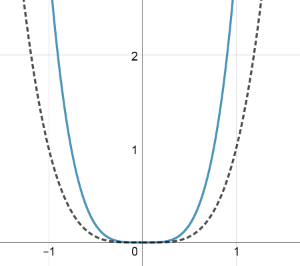
Das folgende Diagramm stellt zum einen den Graphen von (gestrichelt) dar. Der andere Graph gehört zum Funktionsterm . Gib das Intervall an, in dem a liegen muss.
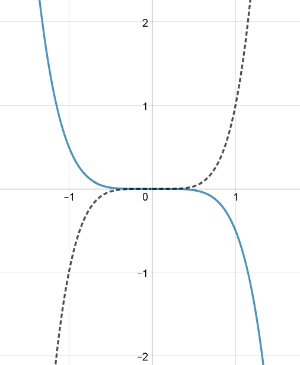
Aufgabe:
Erstelle nun deinen eigenen, übersichtlichen Hefteintrag, der Wesentliches zusammenfassen soll.
Gehe auf folgende Punkte ein:
1.) Wie ist die "allgemeinen Potenzfunktion" definiert ?
2.) Wie hängt der Exponent n mit der Symmetrie des Graphen (und welcher Symmetrie?) zusammen?
3.) Was ist der charakteristische Verlauf des Graphen, in den Fällen I. II, III und IV:
I : n gerade und a > 0
II : n gerade und a < 0
III : n ungerade und a > 0
IV : n ungerade und a < 0
Skizziere jeweils zwei Graphen für jeden der vier Fälle.
4.) Wie ist das Monotonieverhalten, d.h.
in welchem Intervall ist der Graph ansteigend, in welchem abfallend?
5.) Welches sind die Wertemengen in den verschiedenen Fällen?
Du brauchst Hilfe beim Hefteintrag?
Dann kannst du dir am Pult einen Hefteintrag mit Lücken holen.
Auch das Buch hilft (siehe auf S. 144), einen schönen Hefteintrag zu erstellen.
Kontrolliere am Ende mit dem "Muster eines Hefteintrags", ob dein Hefteintrag vollständig ist.