Pytagoras' setning
Pytagoras ( 570 - 495 f.Kr. )

På videoen er det en rettvinkla trekant i midten. På sidene av trekanten er det kvadrater med vann!
Oppgave
Nedenfor er et bilde av en gul rettvinkla trekant i midten. På sidene til trekanten er det laget tre kvadrater.
Dra i gliderne i bildet under og se hva som skjer.
Oppgave
Figuren består av en rettvinkla trekant ABC. Ut fra sidene i trekanten er det tegnet tre kvadrater. (Areal1, Areal 2 og Areal 3).
Dra i punktene A, B og C og se hvordan figuren og arealverdiene forandrer seg. Se også verdiene på regnearket.
Spørsmål 1
Etter at du har sett videoen og de to animasjonene - Kan du si noe om sammenhengen mellom størrelsen på arealene av de tre kvadratene?
Spørsmål 2
Hvordan kan du regne ut hvor lange sidene er i et kvadrat når du vet arealet?
Spørsmål 3
Arealet av et kvadrat er 64. Hvor lange er sidene?
Figuren viser en rettvinkla trekant ABC med sidene AB = 3 cm og AC= 4 cm. Bruk det du har lært til å finne lengden av BC.
Spørsmål 4
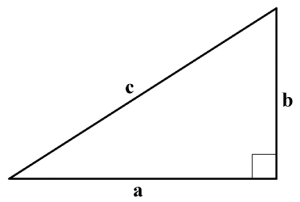
Nå skal du gjøre som Pytagoras! Tenk deg at du har en rettvinkla trekant som den på bildet under. Ut fra det du har funnet ut til nå: Sett opp den matematiske sammenhengen mellom sidene i en rettvinkla trekant.
Bruk bokstavene a, b og c.
Spørsmål 5
Figuren under viser en rettvinkla trekant med tilhørende halvsirkler. Sjekk om Pythagoras også stemmer ved halvsirkler ved å dra i punktene.