Cornu-Spirale
Wie Lichtstrahlen und das Huygens-Prinzip zusammen passen
Mit freundlicher Genehmigung von Michael Rode.

Wer Strahlenoptik gelernt hat, kann mit solchen Bildern viel anfangen. Jede und jeder auch nur ein wenig Beschulte wird durch das Bild zum Zitieren des Reflexionsgesetzes angeregt. Wer etwas mehr gelernt hat, kann auch eine Zeichnung heranziehen:
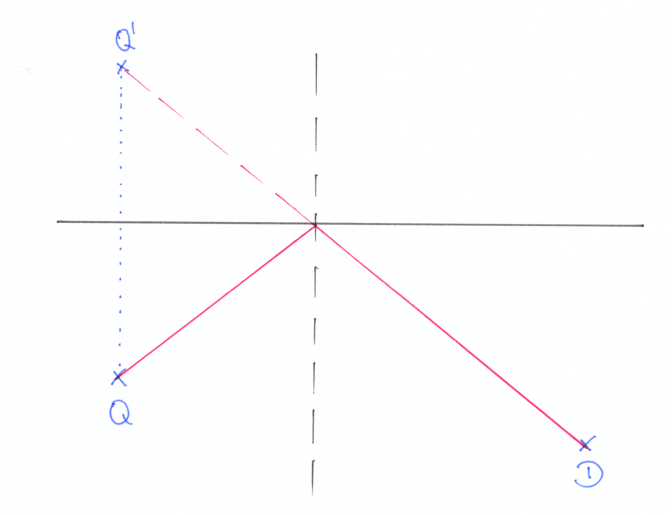
In der Oberstufe soll nun Licht als Wellenphänomen aufgefasst werden und man lernt, dem Huygens-Prinzip entsprechend:
„Jeder Punkt einer Wellenfront wird zum Ausgangspunkt einer Kugelwelle“.
Wer das ernst nimmt, stößt auf Widersprüche zu seinen gewohnten Vorstellungen aus der Strahlenoptik.

Das Licht der Kerze sollte sich doch ausbreiten wie eine Kugelwelle – damit müsste dann aber auch jeder Punkt der Spiegeloberfläche zur Reflexion beitragen. Kann das stimmen?
Am Anfang einer Antwort kann eine Modellation in der Zeigerdarstellung stehen. Wie man Modelle in Zeigerdarstellung in dynamische Geometriedateien umsetzt, wurde in [1] gezeigt.
Das Ergebnis der Modellation nennt man die Cornu-Spirale. Abhängig von der Breite des Spiegels im Verhältnis zur Wellenlänge und von der Wellenlänge selbst sind die beiden „Ohren“ der Spirale mehr oder weniger stark „eingedreht“. Immer ist zu erkennen, dass die resultierende Zeigerlänge im Wesentlichen durch den Mittelteil der Spirale zustande kommt. Die zugehörigen Zeiger gehören alle zu Lichtwegen über den zentralen Teil des Spiegels, einen Bereich von wenigen Wellenlängen Breite um den kürzesten Lichtweg herum. Weil die Wellenlänge des Lichtes so klein ist, funktioniert unter klassischen Bedingungen das Reflexionsgesetz als sehr gute Näherung!
Das Ergebnis der Cornu-Modellation stimmt mit dem Fermatschen Prinzip überein. Nach diesem Prinzip werden ja genau diejenigen Lichtwege beobachtet, für die die Laufzeit extremal ist.
Das sind nun gerade diejenigen Lichtwege, zu denen die Zeiger in der Mitte der Spirale gehören: diese Zeiger zeigen alle annähernd in die gleiche Richtung. Das bedeutet, dass die Änderungsrate der Weglänge/Laufzeit mit dem Ort nahezu null ist – genau das Kriterium für das Vorliegen eines lokalen Extremums!
In [4] wird ein vergleichbares Vorgehen auf die geradlinige Ausbreitung des Lichtes angewandt. Dort wird dargestellt, wieso trotz des Huygens-Prinzips Licht sich geradlinig ausbreiten kann.
Es gibt eine Möglichkeit, die Existenz der Cornu-Spirale bei Licht auch experimentell zu bestätigen.
Dazu wird ein Versuch wie in Abb.5 benutzt.
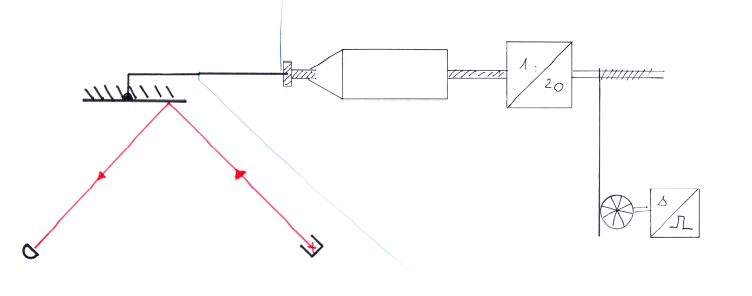
In diesem Experiment „wickelt man die Cornu-Spirale quasi vom Ende her ab“, mit der Folge, dass die Länge des resultierenden Zeigers zunächst periodisch schwankt, um schließlich stetig kürzer zu werden.
Man erhält Messdiagramme wie in Abbildung 6, die schön die erwartete periodische Variation zeigen.
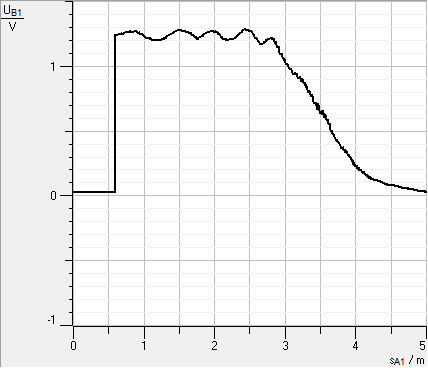
Wenn man den Spiegel an geeigneter Stelle (nämlich in den „Ohren“ der Cornu-Spirale) auskratzt, verhalten sich Spiegel völlig anders. Es ergeben sich Beobachtungen, die das Reflexionsgesetz deutlich verletzen, wie in [2] am Beispiel von Ultraschall ausführlich beschrieben wird.
Bödeker zeigt in [3], wie man solche ausgekratzten Spiegel auch für Licht herstellen kann.
[1] Rode, M.: Schwingungen und Wellen mithilfe der Zeigerdarstellung verstehen. Velber, Friedrich: UP 22/125, 2011. S. 12 ff.
[2] Barth, M.: Interferenzversuche mit Ultraschall. Velber, Friedrich: UP 22/125, 2011. S. 16 ff.
[3] Bödeker, A.: Optik in der Sekundarstufe II. Berlin, PädZeitschriftenverlag. PhiS 35/1997, Heft 4. S.131 ff.
[4] Dorn-Bader Physik, Gymnasium Sek II. Hannover, Schroedel 2000. S. 194 f.
