Definições
Cilindro
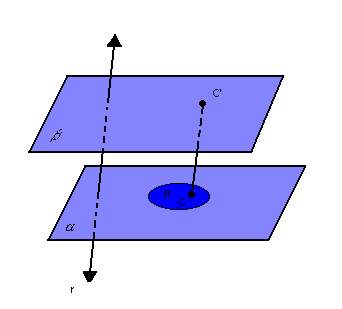
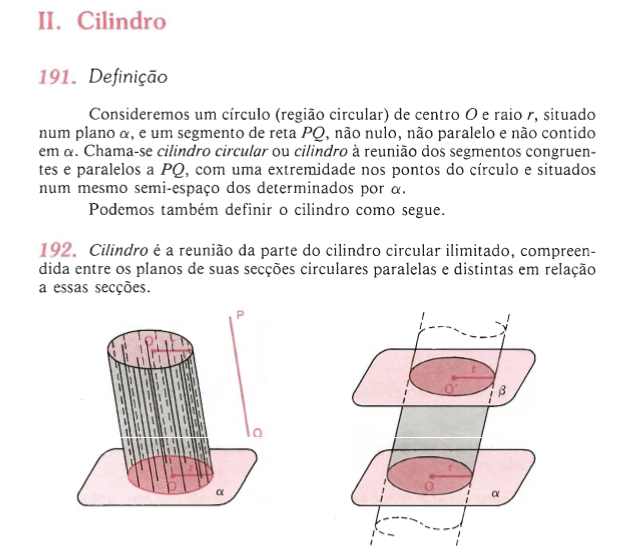
Na figura abaixo, temos dois planos paralelos e distintos,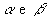 , um círculo R contido em
, um círculo R contido em  e uma reta r que intercepta
e uma reta r que intercepta 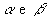 , mas não R:
, mas não R:
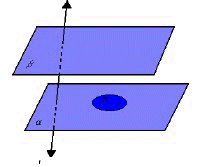 Para cada ponto C da região R, vamos considerar o segmento
Para cada ponto C da região R, vamos considerar o segmento  , paralelo à reta r
, paralelo à reta r 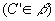 :
:
 Assim, temos:
Assim, temos:
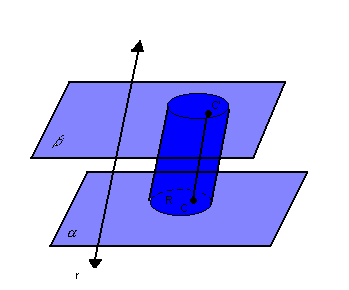 Chamamos de cilindro, ou cilindro circular, o conjunto de todos os segmentos
Chamamos de cilindro, ou cilindro circular, o conjunto de todos os segmentos  congruentes e paralelos a r.
Elementos do cilindro
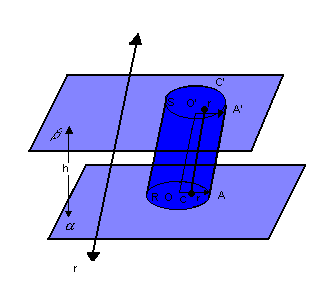
Dado o cilindro a seguir, consideramos os seguintes elementos:
congruentes e paralelos a r.
Elementos do cilindro
Dado o cilindro a seguir, consideramos os seguintes elementos:
 Para cada ponto C da região R, vamos considerar o segmento
Para cada ponto C da região R, vamos considerar o segmento  Assim, temos:
Assim, temos:
 Chamamos de cilindro, ou cilindro circular, o conjunto de todos os segmentos
Chamamos de cilindro, ou cilindro circular, o conjunto de todos os segmentos 
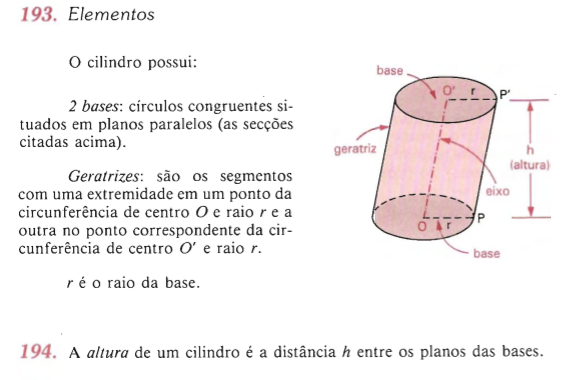
- bases: os círculos de centro O e O'e raios r
- altura: a distância h entre os planos
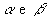
- geratriz: qualquer segmento de extremidades nos pontos das circunferências das bases ( por exemplo,
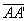 ) e paralelo à reta r
) e paralelo à reta r

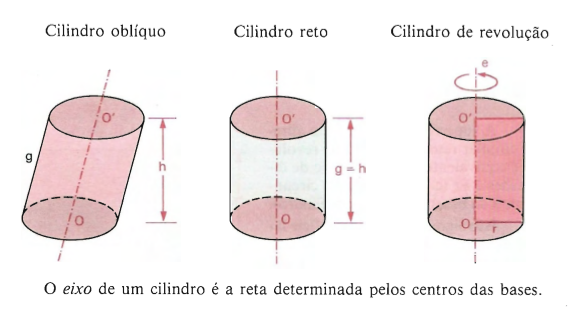
Um cilindro pode ser:


- Circular oblíquo: quando as geratrizes são oblíquas às bases;
- Circular reto: quando as geratrizes são perpendiculares às bases.



Áreas
Num cilindro, consideramos as seguintes áreas:
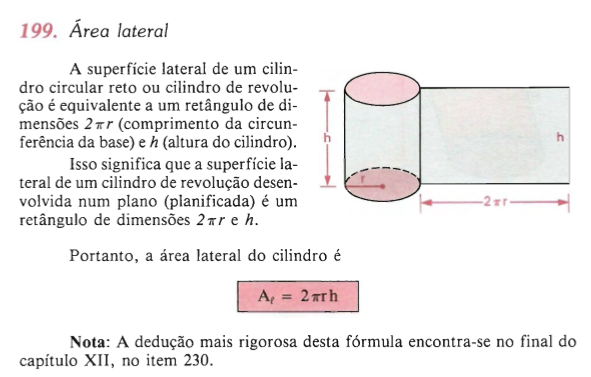
a) área lateral (AL)
Podemos observar a área lateral de um cilindro fazendo a sua planificação:
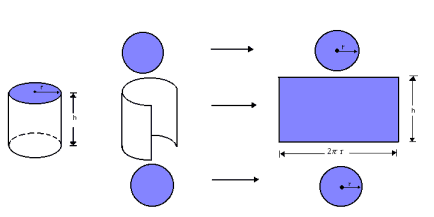 Assim, a área lateral do cilindro reto cuja altura é h e cujos raios dos círculos das bases são r é um retângulo de dimensões
Assim, a área lateral do cilindro reto cuja altura é h e cujos raios dos círculos das bases são r é um retângulo de dimensões 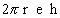 :
:
b) área da base ( AB):área do círculo de raio r
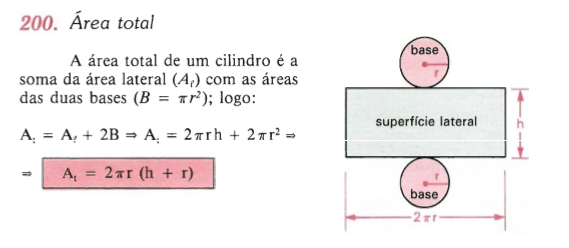
c) área total ( AT): soma da área lateral com as áreas das bases
 Assim, a área lateral do cilindro reto cuja altura é h e cujos raios dos círculos das bases são r é um retângulo de dimensões
Assim, a área lateral do cilindro reto cuja altura é h e cujos raios dos círculos das bases são r é um retângulo de dimensões 
