Progresiones geométricas
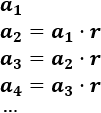Una sucesión geométrica (o progresión geométrica) es una sucesión en la que cada término a(n) se obtiene multiplicando al término anterior a(n-1) por un número r llamado razón.
La razón de una sucesión geométrica se denota por r y debe ser constante en toda la sucesión.
Ejemplo: La sucesión de las potencias de 2 es una sucesión geométrica con razón r=2:
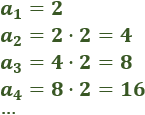El término general de esta sucesión es
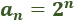La razón de una progresión geométrica se calcula dividiendo términos consecutivos:
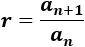El término general de una sucesión geométrica se calcula a partir del primer término a(1) y de la razón r:
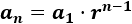Ejemplo: Calculamos el término general de la siguiente progresión geométrica:
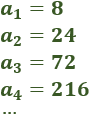La razón de la sucesión es r=3 ya que
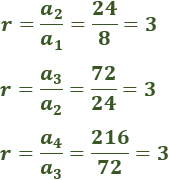El término general de la sucesión es
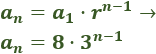Para sumar los primeros n términos de una progresión geométrica disponemos de la fórmula
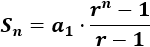Cuando la razón de la progresión es |r|<1 se pueden sumar todos los términos mediante la fórmula
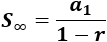
Más información y problemas resueltos de sucesiones:
- Test básico
- Tipos de sucesiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- Sucesión de Fibonacci
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones
- Introducción a las sucesiones (PyE)
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz del cociente