Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

0302 A tükrözési axiómák megjelenítése a P-modellen

Szerző:Szilassi Lajos

1.

  • egy pont tükörképének az ugyanerre az egyenesre vonatkozó tükörképe az eredeti pont;
Involutorikusnak nevezzük azokat a geometriai transzformációkat, amelyeket bármely geometriai alakzatra ,majd a keletkezett képére alkalmazva visszakapjuk az eredeti alakzatot. Ilyen az euklideszi geometriában a tengelyes tükrözés, a középpontos tükrözés, és az inverzió is. Jelen esetben az a kérdés, hogy a P-modellen értelmezett HTükrözés[] involutorikus-e? Elvileg az, hiszen ez a transzformáció - euklideszi értelemben tengelyes tükrözés, vagy inverzió. Mégis indokolt feltenni a kérdést: ugyanez milyen pontosan működik a GeoGebrában, jelesül a P-modellen? Előrebocsátjuk, hogy egy geometriai alakzatok megjelenítését végző  (de a háttérben nyilvánvalóan véges pontosságú számokkal dolgozó) számítógép algebrai rendszer soha nem lehet tökéletesen pontos, így ez a GeoGebrától sem várható el. A Geogebra akkor tekint két pontot azonosnak, ha a koordinátáik különbsége mindkét koordinátára nézve nem nagyobb, mint  a Geogebra rajzlap egységének a 10-8 -szorosa. Ugyanakkor a rajzlap nagyítása (zoomolása) sem folytatható vég nélkül. Addig lehet a rajzlapot nagyítani, amíg a megjelenített rács egysége 10-13 -nál nagyobb. Maga a program 15 tizedesjegynyi pontosan számol, így az ilyen pontosan kiírt számolási eredményekben már előfordulhatnak kimutatható eltérések, amelyek az elegendően erős nagyításnak alávetett rajzlapon már láthatóvá válnak.

Involutorikus-e a HTükrözés?

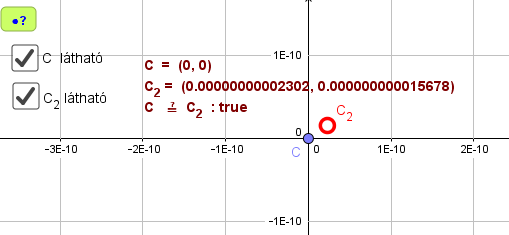
Olvasóinkra bízzuk annak a kísérletnek az elvégzését, hogy a fenti a programban mennyire kellett  „kivinni” az alapkör szélére a t tengelyt ahhoz, hogy előállíthassunk egy olyan képet, amelyen a tükörkép tükörképe a rajzon látható módon ( már) nem esik egybe az eredetivel, noha  (még) egybeesőnek tekinti a GeoGebra a C és a C2 pontot.
Image

2.

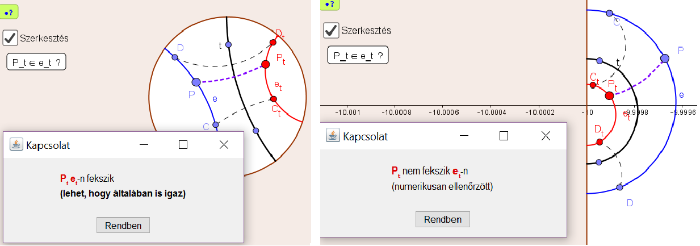
o  Az egy egyenesre eső pontoknak a tükörképei is egy egyenesre esnek; (A tükrözés egyenes-tartó.) Azt vizsgáljuk a P-modellen, hogy ha a P pont illeszkedik az e=(C,D) egyenesre, akkor vajon a P- nek a t=(A,B) egyenesre vonatkozó Pt tükörképe illeszkedik-e az e egyenes et=(At,Bt) tükörképére. Vagyis  a HTükrözés[] eljárás valóban "H-Egyenes”-tartó-e.? Erre a vizsgálatra egy lehetőség kínálkozik. Adjuk meg P pontot a P=Pont[e] paranccsal. Ekkor P illeszkedni fog az e egyenesre. A GeoGebra  Kapcsolat[P_t,e_t] parancsával tudjuk megvizsgálni a Pt és az et objektumok kapcsolatát. Ezt a parancsot most egy gomb segítségével aktivizálhatjuk. Vajon a GeoGebra rajzlap ilyen nagyítása mellett mekkora lehet – mondjuk a Föld méretéhez képest ‑ a P-modell alapköre, amelynek a sugara a rajzlap koordináta rendszerében 10 egység? Akinek - most - nincs kedve ahhoz, hogy számolásra adja a fejét, figyelmébe ajánljuk ezt a weblapot. Itt jegyezzük meg, hogy a GeoGebra rajzlapon a nagyítás, kicsinyítés (zoomolás) funkciója 10-13 és 5 108 között működik. A fenti link tanulmányozása feltehetően meggyőzte olvasóinkat arról, hogy ezzel a pontossággal elégedettek lehetünk.

Egyenestartó-e a HTükrözés?

Meg kell elégednünk az általában megnyugtató, de egészen extrém esetben a látszatnak is ellentmondó nyugtalanító válasszal:

3.

  • Egy tengelyesen szimmetrikus pontpárnak egy egyesre vonatkozó tükörképei is tengelyesen    szimmetrikusak. (A tükrözés szimmetriatartó.)
Lényegében azt kell szemléltetnünk, hogy három egymást követő H-tükrözés eredménye milyen pontosan egyezik meg egy negyedikkel. Tekintsünk most el attól, hogy itt is provokáljunk ki egy ellentmondásos szituációt.
Image

Szimmetria tartó-e a HTükrözés?

Miután láttunk példát és ellenpéldát – mindkét irányban ‑ a P-modell Geogebra rajza és az adott relációra kapott válasz között, megállapodhatunk abban, hogy nem célszerű megszállottan keresnünk ezeket az extrém helyzetekben előbukkanó ellentmondásokat. Megnyugodhatunk: a GeoGebrával szemléltetett P-modell több, mint elegendő pontossággal mutatja be az abszolút-, és hiperbolikus geometria alapjelenségeit.

Új anyagok

Anyagok felfedezése

Témák felfedezése