Afleiden en integreren in het CAS venster
Afleiden en integreren in het CAS venster
In dit werkblad leer je het CAS venster en de knoppen van de knoppenbalk gebruiken om
- de afgeleide functie van een gegeven functie te berekenen
- de primitieve functie van een gegeven functie te berekenen
Leer eerst enkele basisvaardigheden van GeoGebra
Ga naar de introductiehandleiding CAS snelgids. Lees zeker 1.1 t.e.m. 1.3. Je vindt er meer over de knoppen van de knoppenbalk. Als je tijd genoeg hebt, neem je ook de overige paragrafen door.
Zorg dat je tijdens het leren kennis hebt gemaakt met 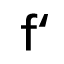 en
en 
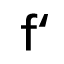 en
en 
Het volgende applet leer je maken
Verken de stapsgewijs de opbouw van onderstaand applet met de knoppen van de navigatiebalk.
Stappenplan
Volg het stappenplan om het bestand op te bouwen in onderstaand scherm.
| | Typ in het invoerveld van het CAS venster het commando f(x) := x³ + x² - 2x en Enter. De grafiek van de functie wordt meteen getoond in het tekenvenster. Let op: Gebruik bij een toewijzing steeds := Het gewone gelijkheidsteken = wordt enkel gebruikt in vergelijkingen.- |
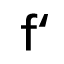
| Typ ) in het tweede invoerveld om de uitvoer van vorige rij te gebruiken als nieuwe invoer en klik daarna op de knop Afleiden om het voorschrift van de afgeleide functie te berekenen. Opmerking: De grafiek van de afgeleide functie wordt nu niet getoond! Wil je de afgeleide functie als een nieuwe functie definiëren, dan moet je een nieuw object definiëren en de formule toewijzen met := |
| | Typ in de derde rij het commando g(x):= Afgeleide[f] om de functie g te definiëren als de afgeleide functie van en de grafiek te tonen. Alternatief: g(x):= Afgeleide[$1] gebruikt een verwijzing naar rij 1 i.p.v. de naam . |

| Klik eerst in het vierde invoerveld en daarna op het functievoorschrift in rij 1. Het voorschrift van verschijnt nu in rij 4 van het CAS venster. Selecteer de knop Integraal om de primitieve functies van te berekenen. Het kan zijn dat eerst de functie met een nieuwe naam verschijnt. Klik dan nogmaals op Integraal. |
Maak het nu zelf...
Lukt het niet, bekijk dan de opbouw in volgend filmpje gemaakt in de offline ggb versie
Je kunt dit filmpje in een grotere schermweergave bekijken op Analyse in het CAS venster.