Función Cuadrática
Introducción a la función cuadrática. Forma polinómica. Elementos de la gráfica de la parábola.
LA FUNCIÓN CUADRÁTICA: FORMA POLINÓMICA
A la función polinómica de segundo grado , siendo y con , se la denomina función cuadrática.
Los términos de la función reciben los siguientes nombres:
término cuadrático
término lineal
término independiente
Puntos característicos de las funciones cuadráticas:
- La representación gráfica de una función cuadrática es una parábola.
- El punto mínimo y máximo de la parábola se denomina vértice. Toda función cuadrática tienen siempre un único vértice, con coordenadas "x" e "y" reales.
- Toda función cuadrática corta al eje "y" en un único punto, denominado ordenada de origen.
- Las raíces son los puntos en donde la parábola interseca al eje x. Una función cuadrática puede tener dos, uno o ninguna raíz real.
1)Funciones de la forma:
La parábola "va" hacia arriba.
La parábola "va" hacia abajo.
La parábola se abre.
La parábola se cierra.
(usa el deslizador "a" y observa el movimiento de la curva)
2)Funciones de la forma:
La gráfica se desplaza hacia arriba.
La gráfica se desplaza hacia abajo.
(usa el deslizador "c" y observa el movimiento de la curva)
3)Funciones de la forma:
Si y tienen el mismo signo, la gráfica se desplaza hacia la izquierda.
Si y tienen el distinto signo, la gráfica se desplaza hacia la derecha.
(usa el deslizador "a" y "b" y observa el movimiento de la curva)
GRÁFICA DE LA PARÁBOLA
Para realizar el gráfico de una parábola, , se deben calcular los elementos de la misma y luego representarla. Podemos ordenar el procedimiento de la siguiente manera:
1° Paso: Obtener raíces de la parábola.
Las raíces de una función, son los valores en los cuáles la función corta el eje de las "x". Cuando una función cuadrática tienen raíces reales, éstas se calculan con la siguiente fórmula:
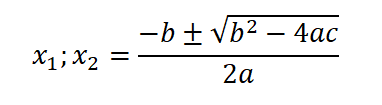
Las raíces son entonces los valores de "x" para los cuales la función vale 0, es decir f(x)=0.
Al radicando se lo llama discriminante, ya que el valor del mismo sirve para discriminar la naturaleza de las raíces y de lo simboliza con la letra griega (delta).
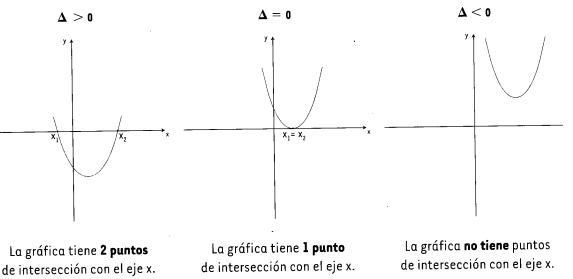
Si Raíces reales distintas.
Si Raíces reales iguales.
Si Raíces no reales.
Las raíces son entonces los valores de "x" para los cuales la función vale 0, es decir f(x)=0.
Al radicando se lo llama discriminante, ya que el valor del mismo sirve para discriminar la naturaleza de las raíces y de lo simboliza con la letra griega (delta).
Si Raíces reales distintas.
Si Raíces reales iguales.
Si Raíces no reales.
 2° Paso: Cálculo de las coordenadas del vértice de la parábola.
Las fórmulas para calcular las coordenadas del vértice son:
2° Paso: Cálculo de las coordenadas del vértice de la parábola.
Las fórmulas para calcular las coordenadas del vértice son:
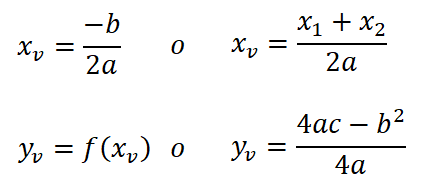
Con estas fórmulas, reemplazando los coeficientes "a", "b" y "c" de la ecuación en forma polinómica, vamos a calcular las coordenadas del vértice. Las coordenadas del vértice son .
3° Paso: trazar eje de simetría.
Es la recta que tiene por ecuación
4° Paso: Intersección con el eje "y"
La intersección con el eje "y", u "ordenada al origen" coincide con el valor del término independiente de la ecuación polinómica, es decir el valor de "c". Es el punto de intersección de la gráfica con el eje y. vale decir f(0)=c.
Con estas fórmulas, reemplazando los coeficientes "a", "b" y "c" de la ecuación en forma polinómica, vamos a calcular las coordenadas del vértice. Las coordenadas del vértice son .
3° Paso: trazar eje de simetría.
Es la recta que tiene por ecuación
4° Paso: Intersección con el eje "y"
La intersección con el eje "y", u "ordenada al origen" coincide con el valor del término independiente de la ecuación polinómica, es decir el valor de "c". Es el punto de intersección de la gráfica con el eje y. vale decir f(0)=c.
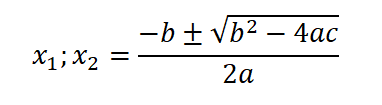
Las raíces son entonces los valores de "x" para los cuales la función vale 0, es decir f(x)=0.
Al radicando se lo llama discriminante, ya que el valor del mismo sirve para discriminar la naturaleza de las raíces y de lo simboliza con la letra griega (delta).
Si Raíces reales distintas.
Si Raíces reales iguales.
Si Raíces no reales.
Las raíces son entonces los valores de "x" para los cuales la función vale 0, es decir f(x)=0.
Al radicando se lo llama discriminante, ya que el valor del mismo sirve para discriminar la naturaleza de las raíces y de lo simboliza con la letra griega (delta).
Si Raíces reales distintas.
Si Raíces reales iguales.
Si Raíces no reales.
 2° Paso: Cálculo de las coordenadas del vértice de la parábola.
Las fórmulas para calcular las coordenadas del vértice son:
2° Paso: Cálculo de las coordenadas del vértice de la parábola.
Las fórmulas para calcular las coordenadas del vértice son:
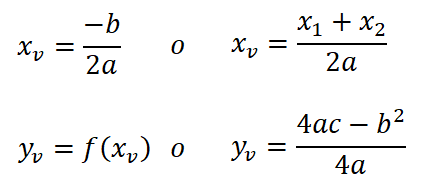
Con estas fórmulas, reemplazando los coeficientes "a", "b" y "c" de la ecuación en forma polinómica, vamos a calcular las coordenadas del vértice. Las coordenadas del vértice son .
3° Paso: trazar eje de simetría.
Es la recta que tiene por ecuación
4° Paso: Intersección con el eje "y"
La intersección con el eje "y", u "ordenada al origen" coincide con el valor del término independiente de la ecuación polinómica, es decir el valor de "c". Es el punto de intersección de la gráfica con el eje y. vale decir f(0)=c.
Con estas fórmulas, reemplazando los coeficientes "a", "b" y "c" de la ecuación en forma polinómica, vamos a calcular las coordenadas del vértice. Las coordenadas del vértice son .
3° Paso: trazar eje de simetría.
Es la recta que tiene por ecuación
4° Paso: Intersección con el eje "y"
La intersección con el eje "y", u "ordenada al origen" coincide con el valor del término independiente de la ecuación polinómica, es decir el valor de "c". Es el punto de intersección de la gráfica con el eje y. vale decir f(0)=c.
Gráfica de la función cuadrática - paso a paso
Actividades:
Ahora te desafío que encuentres las raíces, el vértice, el eje de simetría y la ordenada de origen de las siguientes funciones cuadráticas:
a)
b)
c)
d) (Dato: tienes que desarrollar el binomio cuadrado perfecto para obtener los valores de a,b y c: )
Luego, con los datos obtenidos puedes corroborar con la siguiente graficadora si los valores obtenidos son los correctos. Para ello, Utiliza los deslizadores a, b y c.
BIBLIOGRAFÍA
1. Matemática 1 polimodal serie Activa Editorial Puerto de Palos (2010).
2. Libros de matemáticas a medida - Ediciones logikamente.