7.5 Los Cuatro Espacios Fundamentales
Imagen Simultanea de los Cuatro Espacios
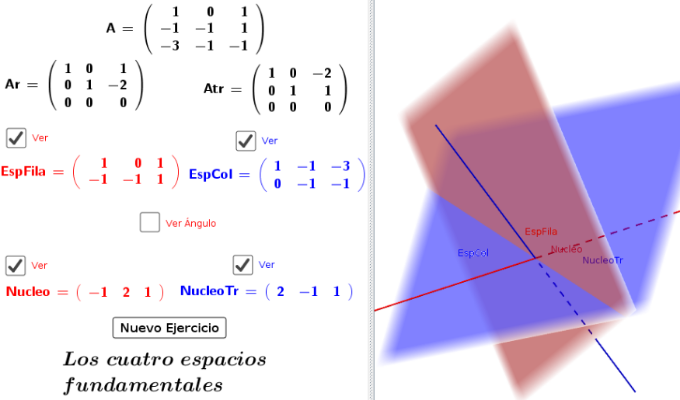
Introducción
En diferentes momentos, va a ser importante pensar en las matrices como vectores. Son vectores con n componentes (si la matriz tiene filas o columnas de tamaño n) Hay importantes espacios vectoriales dentro de . Esos son subespacios de . Comience con el espacio tridimensional habitual . Elija un plano a través del origen (0, 0, 0). Ese plano es un espacio vectorial por derecho propio. Si agregamos dos vectores en el plano, su suma está en el plano. Si multiplicamos un vector en el plano por 2 o -5, todavía se está en el plano. Un plano en un espacio tridimensional no es (incluso si parece ). Los vectores tienen tres componentes y pertenecen a . El plano es un espacio vectorial dentro de . Esto ilustra una de las ideas fundamentales en álgebra lineal. El plano pasa a través de (0, 0, 0) y es un subespacio del espacio vectorial completo ( ).
Cualquier combinación de dos vectores en un plano por (0,0,0) permanece en el plano