Ejercicio 19. El triángulo de Sierpinski
El matemático Waclaw Sierpinski, fue un importante matemático polaco que dedicó una parte de sus investigaciones al estudio de distintas formas de fractales (introdujo el que analizaremos en 1919), hoy nos centraremos en una de las más conocidas.

El triángulo de Sierpinski se puede descomponer en tres figuras congruentes. Cada una de ellas con exactamente la mitad de tamaño de la original. Si doblamos el tamaño de una de las partes recuperamos el triángulo inicial. El triángulo de Sierpinski está formado por tres copias autosimilares de él mismo. Decimos que es autosimilar (propiedades especifica de los fractales).
Se debe aclarar que se puede construir a partir de cualquier triángulo (para los ejemplos se utilizan triángulos equiláteros, dado que las construcciones son más bellas), y que no hay un único método para hacerlo; ya que como en la mayoría de los fractales, existen varias maneras de obtener la misma figura.
Es por ello que explicaremos dos métodos totalmente diferentes
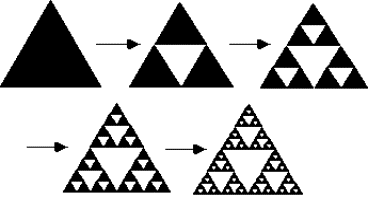
Construcción por Iteración
Partamos (iteración n=0) de la superficie de un triángulo equilátero de lado unidad. Seguidamente (iteración n=1) tomamos los puntos medios de cada lado y construyamos a partir de ellos un triángulo equilátero invertido de lado 1/2. Lo recortamos. Ahora (iteración n=2) repetimos el proceso con cada uno de los tres triángulos de lado 1/2 que nos quedan. Así que recortamos, esta vez, tres triángulos invertidos de lado 1/4.

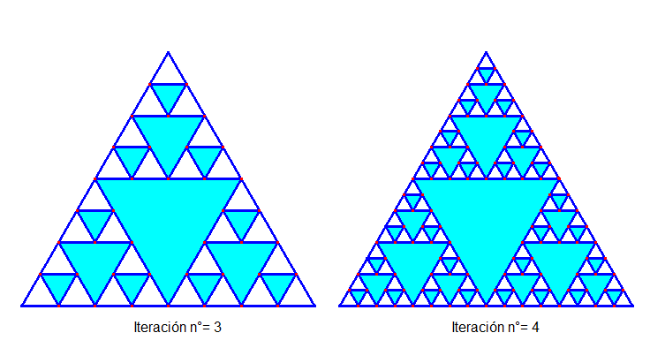
En las imágenes observamos hasta cuatro iteraciones sucesivas. Si repetimos infinitamente el proceso obtendremos una figura fractal denominada triángulo de Sierpinski.
Todo lo anterior lo podemos observar en el Applet de Geogebra que esta al inicio, dando clic en el botón de iteración 1, iteración 2, iteración 3, de manera que puedas visualizar la construcción del triángulo de Sierpinski .