4.2. Domínio, contradomínio e imagem de uma função
A lei de formação que intitula uma determinada função, possui três características básicas: domínio, contradomínio e imagem. Essas características podem ser representadas por um diagrama de flechas, como mostra a imagem a seguir:
Dada a seguinte função f(x) = x + 1, e os conjuntos A(1, 2, 3, 4, 5) e B(1, 2, 3, 4, 5, 6, 7). Vamos construir o diagrama de flechas:
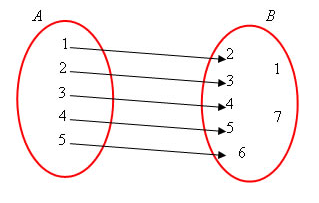
Nessa situação, temos que:
O domínio de uma função de A em B é sempre o próprio conjunto de partida, ou seja, D=A. Se um elemento x 
A estiver associado a um elemento y B, dizemos que y é a imagem de x (indica-se y=f(x) e lê-se “y é igual a f de x”).
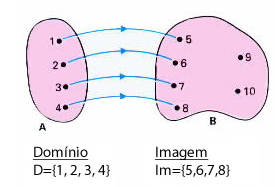
Observe o domínio e a imagem na função abaixo.
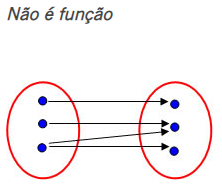
Todos os elementos do conjunto domínio devem possuir representação no conjunto do contradomínio. Caso isso não ocorra, a lei de formação não pode ser uma função.
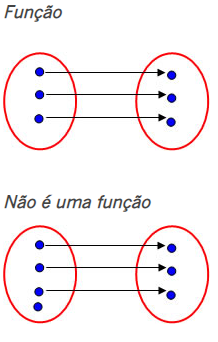
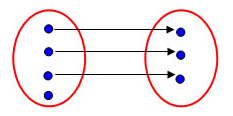
Restam elementos no conjunto domínio, que não foram associados ao conjunto imagem.
Um único elemento do domínio não deve possuir duas imagens.
Marcela foi comprar bombons na confeitaria. Cada bombom custa R$1,80. A quantia que ela pagará ( y) será função do número de bombons que levar (x), pois, para cada quantidade de bombons, há um único preço a ser cobrado.
Os valores de x para essa função são números naturais. Não se compra 2,3 bombons. Dizemos que o domínio dessa função é o conjunto dos números naturais. Nessa função, x pode ser qualquer número natural, mas x não pode ser uma fração ou número negativo. Observando a tabela, vemos que quando x = 3, temos y = 5,40. Diremos que 5,40 é a imagem de 3 por esta função.
Ariel pensou em uma função que associa um número x ao seu dobro y (y = 2x).
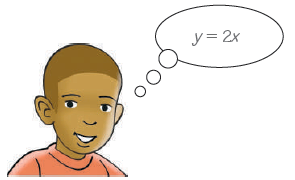
Existe algum número que não possui dobro? Não, então nessa função, x pode ser qualquer número real, pois é sempre possível calcular o dobro de um número. Diremos, então, que o domínio da função pensada pelo Ariel é .
No entanto, se a função associasse, por exemplo, cada número x ao seu inverso y (y = ), teríamos de excluir do domínio o número zero, pois zero é o único número real que não possui inverso.
Em geral, quando não se explicita qual é o domínio de uma função, consideramos o domínio como , tomando o cuidado de excluir, se necessário, números para os quais não exista y correspondente a ele pela função.