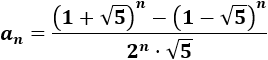Sucesión de Fibonacci
Introducción
La sucesión de Fibonacci es conocida desde hace miles de años, pero fue Fibonacci (Leonardo de Pisa) quien la dio a conocer al utilizarla para resolver un problema.
El primer y segundo término de la sucesión son
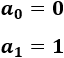 Los siguientes términos se obtienen sumando los dos términos que les preceden:
El tercer término de la sucesión es
Los siguientes términos se obtienen sumando los dos términos que les preceden:
El tercer término de la sucesión es
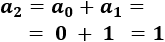 El cuarto término es
El cuarto término es
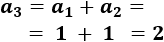 El quinto término es
El quinto término es
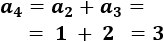 El sexto término es
El sexto término es
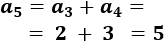 El (n+1)-ésimo término es
El (n+1)-ésimo término es
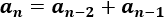
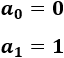 Los siguientes términos se obtienen sumando los dos términos que les preceden:
El tercer término de la sucesión es
Los siguientes términos se obtienen sumando los dos términos que les preceden:
El tercer término de la sucesión es
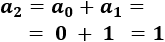 El cuarto término es
El cuarto término es
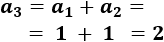 El quinto término es
El quinto término es
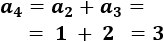 El sexto término es
El sexto término es
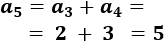 El (n+1)-ésimo término es
El (n+1)-ésimo término es
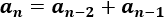
Término general
La sucesión de Fibonacci es una sucesión definida por recurrencia. Esto significa que para calcular un término de la sucesión se necesitan los términos que le preceden.
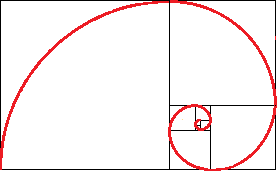
Se proporcionan los dos primeros términos: a(0)=0 y a(1)=1. Los siguientes se calculan con la siguiente fórmula:
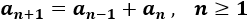 Problemas propuestos:
Problemas propuestos:
 Problemas propuestos:
Problemas propuestos:
- Problema 1: Calcular los 15 primeros términos de la sucesión de Fibonacci.
- Problema 2: ¿Es una sucesión aritmética? ¿Y geométrica? ¿Por qué?
- Problema 3: ¿Es una sucesión creciente, decreciente o alternada? ¿Por qué?
- Problema 4: ¿La suma todos los términos de la sucesión es un número finito como en algunas progresiones geométricas?
- Problema 5: La espiral de Fibonacci se traza uniendo dos vértices de cuadrados adosados. La longitud del lado de los cuadrados viene dada por la sucesión de Fibonacci. ¿Cuánto miden los lados de los 9 cuadrados de la figura?

Más información y problemas resueltos de sucesiones:
- Test básico
- Tipos de sucesiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- Sucesión de Fibonacci
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones
- Introducción a las sucesiones (PyE)
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz del cociente
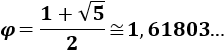
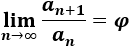 Esto significa que los cocientes de los términos consecutivos de la sucesión de Fibonacci se aproximan al número áureo.
Esto significa que los cocientes de los términos consecutivos de la sucesión de Fibonacci se aproximan al número áureo.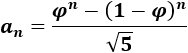 Operando un poco,
Operando un poco,