Розробка та застосування моделей для дослідження елементарних функцій
Постійна функція
Постійна функція на множині всіх дійсних чисел задається формулою y=C, де C – дійсне
число. Графіком постійної функції є пряма, яка є паралельною осі абсцис і
проходить через точку з координатами (0,C) [11].
Задача на побудову 1. Побудувати модель графіка постійної функції.
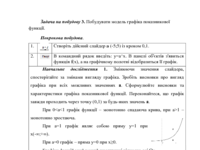
Степенева функція
Степенева функція – математична функція виду y=xn, де n (показник степеня) – дійсне число. До степеневих часто відносять
і функцію виду y=kxn, де k – масштабний множник, коефіцієнт.
Задача на побудову 2. Побудувати модель графіка степеневої функції.
Навчальне дослідження 1. Змінюючи значення обох слайдерів, спостерігайте за
змінами графіка. Зробіть висновки про вигляд графіка при n<0, n=0, n=1, n>1. Поставте у властивостях слайдера n крок на значення 0,1. Який вигляд має графік при дробовій степені
n? Як впливає на вигляд графіка
параметр k?
Навчальне дослідження 2. Чому на наведеному вище зображенні графіки функцій з
різними степенями, що накладаються один на одного, утворюють «пучки» в трьох
точках?
Показникова функція
Показникова функція – математична функція виду y=ax, де a – основа степеня, а x
– показник степеня.
У загальному вигляді – uv, була введена Лейбніцем в 1695 г.
Особливо виділяється випадок, коли в якості основи степеня виступає число e≈2,7. Така функція називається експонентою.
Задача на побудову 3. Побудувати модель графіка показникової функції.
Навчальне дослідження 1. Змінюючи значення
слайдера, спостерігайте за змінами вигляду графіка. Зробіть висновки про вигляд
графіка при всіх можливих значеннях а.
Сформулюйте висновки та характеристики графіка показникової функції.
Переконайтеся, що графік завжди проходить через точку (0,1) за будь-яких
значень а.
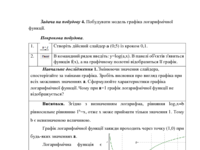
Логарифмічна функція
Нагадаємо, що функція виду y =logaх (де а >0, а ≠ 1) називається логарифмічною.
Задача на побудову 4. Побудувати модель графіка логарифмічної функції.
Навчальне дослідження 1. Змінюючи значення слайдера, спостерігайте за змінами
графіка. Зробіть висновки про вигляд графіка при всіх можливих значеннях а. Сформулюйте характеристики графіка
логарифмічної функції. Чому
при а=1 графік логарифмічної функції
не відображується?
Тригонометричні функції
Нагадаємо, що тригонометричні функції – математичні
функції від кута. Історично вони виникли при вивченні прямокутних трикутників і
виражали залежності довжин катетів цих трикутників від гострих кутів при
гіпотенузі [12].
Виділяють чотири основні тригонометричні функції:
синус: y=sin α;
косинус: y=cos α;
тангенс y=tg α;
котангенс: y=ctg α;
sin α і cos α –це прямі тригонометричні функції;
tg α і ctg α є похідними від них.
У шкільному курсі геометрії тригонометричні функції
гострого кута визначаються як відносини сторін прямокутного трикутника:
синус– протилежного катета до гіпотенузи.
косинус– прилеглого катета до гіпотенузи.
тангенс– протилежного катета до прилеглого.
котангенс– прилеглого катета до протилежного.
У цьому розділі описано побудову графіків тригонометричних функцій засобами GeoGebra.
Задача на побудову 5. Побудувати моделі графіків тригонометричних функцій.
Навчальне дослідження 1. Для кожної функції
створіть слайдери коефіцієнтів. Наприклад, для графіка синуса додайте
коефіцієнти a, b і c:
y=a*sin(b*x+c). Спостерігайте за змінами графіків функцій, змінюючи
значення слайдерів. Переконайтесь, що параметр а визначається як амплітуда функції. За визначенням, амплітуда – це
найбільше значення, яке приймає певна величина, що змінюється за гармонійним
законом (в даному випадку, тригонометрична функція) [13],
а параметр b визначає період функції Т.