Grafisches Lösen quadratischer Gleichungen - Unterrichtsplanung
Kurzinformation
- Thema: Quadratische Gleichungen
- 9. Schulstufe, Mathematik
- Dauer: 2 Einheiten
- SchülerInnenmaterial: Geogebrabuch
- Spezielle Materialien: 3 Laptops mit Geogebra, Puzzle zur quadratischen Ergänzung
Vorwissen und Voraussetzungen
Die SchülerInnen...
- ...können Wertetabellen erstellen und Punkte in ein Koordinatensystem eintragen
- ...können Gleichungen umformen und vereinfachen
- ...haben Grundkenntnisse mit Geogebra
Lernergebnisse und Kompetenzen
Die SchülerInnen können...
- ...Lösungen als Schnittpunkte von Funktionen grafisch ermitteln
- ...Lösungen als Schnittpunkte eines Thaleskreises mit der X-Achse ermitteln
- ...die grafische Interpretation der quadratischen Ergänzung nutzen um Lösungen zu ermitteln
Unterrichtsablauf
Die gesamte Sequenz besteht aus zwei Unterrichtseinheiten.
1.Einheit
In der ersten Einheit werden die geplanten grafischen Lösungsmethoden vom LehrerIn wiederholt oder teilweise eingeführt. Zur Wiederholung zählt die Bestimmung von Schnittpunkten zwischen Funktionen. Neu besprochen wird die quadratische Ergänzung und die grafische Lösung über den Sehnensatz und den Satz von Vieta.
2.Einheit
In der zweiten Einheit werden die zuvor genannten Lösungsmethoden von den SchülerInnen erprobt und geübt. Zu diesem Zweck dient ein Stationenbetrieb, der in 3er-Gruppen bearbeitet wird. Jede Station behandelt dabei eine Lösungsmethode und jeder SchülerIn bekommt zur Orientierung ein Übersichtsblatt.
Pflichtstation 1 (15 min) und 2 (15 min)
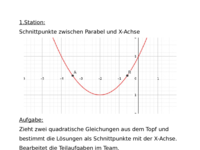
Mit den ersten beiden Stationen sollen die SchülerInnen die grafische Darstellung von Gleichungen wiederholen. Als erstes wird eine Gleichung gezogen. (Station 1: ax²+bx+c=0 und Station 2: x²=kx+d). Danach wird die linke und rechte Seite als Funktion aufgefasst und eine Wertetabelle angelegt. Die berechneten Punkte werden dann in das Koordinatensystem eingetragen und die gesuchten Schnittpunkte abgelesen. Zur Kontrolle werden die Schnittpunkte am Ende mit Geogebra ermittelt.
Didaktischer Kommentar:
Die SchülerInnen sollen sich Bekanntes in Erinnerung rufen (Wertetabellen, zeichnen von Graphen) und die Zeitersparnis durch Technologieeinsatz schätzen lernen. Außerdem soll der Vergleich von Station 1 und 2 zeigen, dass es leichter ist eine Normalparabel und eine Gerade zu zeichnen, als eine verschobene gestauchte Parabel. Der Topf aus dem gezogen wird, kann ein beliebiges Behältnis sein.
Pflichtstation 3 (15 min)
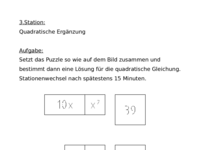
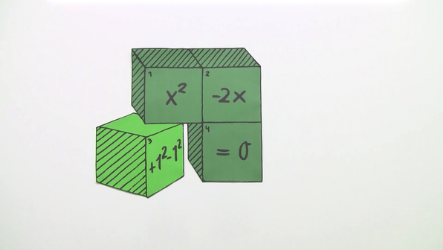
Mit der dritten Station wird das Prinzip der quadratischen Ergänzung durch ein Puzzle-Spiel veranschaulicht. Es gibt drei verschiedene Gleichungen. Jede Gleichung wird durch einen eigenen Puzzlesatz beschrieben. Die grafische Darstellung der quadratischen Ergänzung muss dabei von den SchülerInnen rekonstruiert werden um die Gleichung auf ein vollständiges Quadrat zu erweitern. Ist das Puzzle zusammengesetzt, können die SchülerInnen die Lösung ohne weitere Hilfsmittel ermitteln. Zur Durchführung gibt es zwei Möglichkeiten.
Modus 1: Jedes der drei Gruppenmitglieder bearbeitet sein eigenes Puzzle
Modus 2: Die Gruppe löst die Puzzles nacheinander
Didaktischer Kommentar:
Mit dem Puzzle-Spiel soll das Schema der quadratischen Ergänzung gezeigt werden. Bei der Fertigung des Spiels wurde wenig Rücksicht auf die exakte Übereinstimmung der Abmessungen der Flächeninhalte genommen. Da jedes Spiel beinahe identisch aussieht, ist der Spieler gezwungen sich hauptsächlich an den Zahlen zu orientieren, die den Flächeninhalt beschreiben. Und auf diese Weise ist der Fertigungsaufwand nicht zu sehr ausgeartet. Je nachdem auf welche Art die Puzzleteile zugeschnitten werden, kann der Schwierigkeitsgrad zu- oder abnehmen.
Bonusstation
Mit der vierten Station soll die Lösungsmethode mit Zirkel und Lineal wiederholt werden. Zur Veranschaulichung dient ein konkretes Beispiel das auch im Applet "x²+10x-39=0" ausgeführt wurde. Die Aufgabe besteht darin die Methode mit dem Sehnensatz und dem Satz von Vieta zu begründen. Als Hilfestellung soll das Lösungsblatt am Lehrertisch zu Verfügung stehen.
Didaktischer Kommentar:
Die Lösung quadratischer Gleichungen mittels Sehnensatz geht über den Pflichtteil hinaus. Diese Station ist zeitlich nicht begrenzt, dient zum Erkenntnisgewinn und als Lückenfüller.
Sicherung / Hausübung
Die Hausübung besteht in der Wiederholung der Lösungsmethoden. Die Aufgaben zur Station 1 und 2 dürfen mit Geogebra gelöst werden. Aufgaben zu den Stationen 3 und 4 werden ohne Geogebra gelöst. Die Lösungen befinden sich hier.
Überprüfen des Lernerfolges
Der Lernerfolg während der Unterrichtssequenz kann z.B. durch die ausgefüllten Wertetabellen und Koordinatensysteme in Station 1, oder durch die richtig zusammengebauten Puzzles in Station 3 überprüft werden.
Der Lernerfolg nach der Unterrichtssequenz kann z.B. durch die Mitschriften aus dem Stationenbetrieb oder durch die Kontrolle der Hausübungen überprüft werden.
Links zu Materialien und Quellen
Material:
Quellen:
- Mathematik lehren, Heft 93, Dezember 2015, Seite 26-31;
- Das Erbe von Vieta (Entnommen am 13.10.18, 16:03)
- Barzel, B., Büchter, A., Leuders, T. (2018). Mathematik-Methodik: Handbuch für die Sekundarstufe I und II. 9. Auflage. Berlin: Cornelsen Verlag GmbH.
- Lernzirkel Quadratische Gleichungen (Entnommen am 13.10.18, 15:07)
- Leitprogramm Quadratische Gleichungen (Entnommen am 13.10.18, 15:31)