Taller de Conjuntos Numéricos
Introducción a la Lección sobre Conjuntos Numéricos
Bienvenidos a nuestra lección sobre conjuntos numéricos. Hoy vamos a embarcarnos en un fascinante viaje a través del mundo de los números, explorando los diferentes tipos de conjuntos numéricos y cómo se relacionan entre sí. Los números son la base de la matemática y entender sus distintos conjuntos nos ayudará a comprender mejor el universo matemático y sus aplicaciones en la vida real.
Objetivo de la lección
Al final de esta lección, tendrás una comprensión clara de los diferentes tipos de conjuntos numéricos y cómo se utilizan en diversos contextos matemáticos y en la vida diaria.
¡Prepárate para explorar el fascinante mundo de los números!
Conjuntos Numéricos: Explicación Detallada
¿Qué son los números naturales?
Los números naturales son los números que utilizas de manera más común en la vida diaria. Son aquellos que usas para contar cosas. Por ejemplo, si cuentas las manzanas en una canasta, dirías: 1, 2, 3, 4, y así sucesivamente. Estos números, 1, 2, 3, 4, etc., son números naturales.
Características de los números naturales:
- Comienzan con el 1: Algunas personas incluyen al 0 en los números naturales, pero tradicionalmente, comenzamos con el 1. Siempre son positivos: No encontrarás números naturales que sean negativos o fracciones. Por ejemplo, -3 o no son números naturales. No tienen fin: Puedes seguir contando números naturales para siempre. Después de 1 viene 2, luego 3, y así sucesivamente, sin fin.
- Los números naturales fueron probablemente los primeros que la humanidad comenzó a usar.
- En matemáticas, el conjunto de todos los números naturales se representa con la letra "".
- Si tienes 5 manzanas, estás usando el número natural 5 para describir cuántas manzanas tienes.
- Si estás en el tercer piso de un edificio, el número 3 es un número natural que indica tu posición en el edificio.
Quiz de Números Naturales - Parte 1
¿Cuál de las siguientes opciones es un número natural?
Quiz de Números Naturales - Parte 2
¿Cuál de las siguientes opciones NO es un número natural?
¿Qué son los números enteros?
Los números enteros son como una extensión de los números naturales que ya conoces, pero con una gran diferencia: incluyen los números negativos y el cero. Entonces, mientras que los números naturales son , etc., los números enteros son
Características de los números enteros:
- Incluyen el cero: A diferencia de los números naturales, el conjunto de los números enteros incluye el 0.
- Números positivos y negativos: Además de los números positivos (como en los números naturales), también tienes números negativos, como -1, -2, -3, etc.
- No son fracciones ni decimales: Al igual que los números naturales, los enteros no incluyen fracciones ni números decimales. Por ejemplo, o 3.5 no son números enteros.
- También son infinitos: Puedes contar indefinidamente en ambas direcciones, positiva y negativa.
- Si estás midiendo la temperatura y esta puede ser de -5 grados (un número entero negativo) o de 15 grados (un número entero positivo).
- En tu cuenta bancaria, un depósito puede representarse con un número entero positivo y un retiro con un número entero negativo.
- La idea de los números negativos fue inicialmente rechazada por muchos, ya que era difícil entender el concepto de "menos que nada".
- En matemáticas, el conjunto de todos los números enteros se representa con la letra " ", que proviene de la palabra alemana "Zahlen" que significa "números".
- Si subes 3 pisos, podrías decir que subiste +3 pisos. Si bajas 3 pisos, sería como bajar -3 pisos.
- En un juego, si ganas 5 puntos, tu puntuación aumenta en +5. Si pierdes 5 puntos, tu puntuación disminuye en -5.
- Números como 2.5 o no son enteros porque son fracciones o decimales.
- Cosas que no se pueden medir en unidades completas, por ejemplo, cuando cocinas esa receta que solo lleva media taza de leche.
Quiz de Números Enteros - Parte 1
¿Cuál de las siguientes opciones es un número entero?
Quiz de Números Enteros - Parte 2
¿Cuál de las siguientes opciones NO es un número entero?
¿Qué son los números racionales?
Los números racionales son todos aquellos números que pueden expresarse como el cociente o la división de dos números enteros, donde el denominador (el número abajo en la división) es diferente de cero. En otras palabras, si puedes escribir un número como una fracción donde tanto el numerador (el número de arriba) como el denominador son enteros, entonces es un número racional.
Características de los números racionales:
- Incluyen fracciones y enteros: Todos los números enteros son también racionales, ya que pueden expresarse como una fracción (por ejemplo, 5 es lo mismo que ).
- Pueden ser positivos o negativos: Al igual que los enteros, los números racionales pueden ser positivos o negativos.
- Decimales finitos y periódicos: Los números racionales incluyen decimales finitos (como 0.75) y decimales periódicos (como ).
- Densidad: Entre cualquier par de números racionales, siempre hay infinitos números racionales. Esto significa que están muy "apretados" o "densos" en la línea numérica.
- Al dividir una pizza en partes iguales, podrías terminar con fracciones de pizza (como o de pizza).
- En finanzas, cuando calculas intereses o proporciones.
- Al realizar recetas de cocina se suelen usar fracciones de otras cantidades, como media taza de leche, o media cucharada de sal.
- La palabra "racional" proviene de "ratio", que significa "cociente" en latín. El conjunto de números racionales se representa con la letra "", que proviene de "quotient" (cociente en alemán).
- Si tienes que repartir $50 entre 4 personas, cada persona recibe $12.50, lo cual es un número racional.
- Medir distancias o longitudes que no son enteras, como 1.5 metros o de kilómetro.
- Números como o no son racionales porque no pueden expresarse exactamente como la división de dos números enteros.
- Los números irracionales, que tienen decimales no periódicos y no terminan, tampoco son racionales.
- Los números irracionales, que tienen decimales no periódicos y no terminan, tampoco son racionales.
Quiz de Números Racionales - Parte 1
¿Cuál de las siguientes opciones es un número racional?
Quiz de Números Racionales - Parte 2
¿Cuál de las siguientes opciones NO es un número racional?
¿Qué son los números irracionales?
Los números irracionales son aquellos números que no pueden expresarse como el cociente (o fracción) de dos números enteros. Esto significa que no pueden escribirse como una fracción simple. Una característica distintiva de los números irracionales es que tienen expansiones decimales infinitas no periódicas. Esto significa que sus decimales siguen sin fin y sin repetir un patrón.
Características de los números irracionales:
- Decimales infinitos no repetitivos: A diferencia de los números racionales, los irracionales tienen decimales que no terminan ni forman un patrón repetitivo.
- No se pueden expresar como fracciones: No hay manera de escribir un número irracional como una fracción de dos enteros.
- Famosos ejemplos: Algunos de los números irracionales más conocidos son y .
- Densidad: Al igual que los racionales, entre cualquier par de números irracionales (y también entre racionales) hay infinitos números irracionales.
- En geometría, π es esencial para calcular el área y la circunferencia de un círculo.
- En ingeniería y física, números irracionales como e (la base del logaritmo natural) son fundamentales.
- La existencia de números irracionales fue descubierta por los antiguos griegos. La historia cuenta que la idea de que la raíz cuadrada de 2 era irracional fue tan perturbadora que se mantuvo en secreto.
- Los números irracionales son un ejemplo fascinante de cómo la matemática puede describir conceptos que parecen desafiar la intuición.
- La longitud de la diagonal de un cuadrado con lados de longitud 1 es , un número irracional.
- El número π, que aparece al medir la relación entre la circunferencia y el diámetro de un círculo, es irracional.
- Cualquier número que pueda expresarse como una fracción de dos enteros no es irracional.
- Los números con decimales que terminan o que se repiten periódicamente son racionales, no irracionales.
Identificación de Números Irracionales - Parte 1
¿Cuál de las siguientes opciones es un número irracional?
Identificación de Números Irracionales - Parte 2
¿Cuál de las siguientes opciones NO es un número irracional?
¿Qué son los números reales?
Los números reales incluyen todos los números que puedes encontrar en la línea numérica. Esto abarca tanto los números racionales (como los naturales, los enteros y las fracciones) como los irracionales (como y ). En esencia, cualquier número que puedas representar en una línea continua es un número real.
Características de los números reales:
- Incluyen racionales e irracionales: Todos los números, ya sean fracciones, enteros, decimales finitos, decimales infinitos no periódicos, etc., son parte de los números reales.
- Pueden ser positivos o negativos: Al igual que los enteros y los racionales, los números reales pueden ser mayores o menores que cero.
- Representan puntos en una línea: Cada número real corresponde a un punto único en la línea numérica.
- Continuidad: A diferencia de los números enteros, que tienen "saltos" entre ellos, los números reales forman una línea continua sin interrupciones.
- Medir con precisión, como en la longitud, el área, el volumen, la temperatura, etc.
- Representar datos en gráficos y en el cálculo.
- Modelar situaciones en física, ingeniería, economía, y muchas otras disciplinas.
- El concepto de números reales se desarrolló a lo largo del tiempo, con contribuciones significativas de matemáticos como Euclides, René Descartes y otros.
- La "completitud" de los números reales es una propiedad importante: cualquier "hueco" en la línea numérica está lleno por un número real.
- La temperatura, que puede ser un número entero, decimal, positivo o negativo, es un ejemplo de número real. Las medidas de longitud, como 1.83 metros o metros, son números reales.
Identificación de Números Reales
De las opciones siguientes, marca todas aquellas que representen números reales
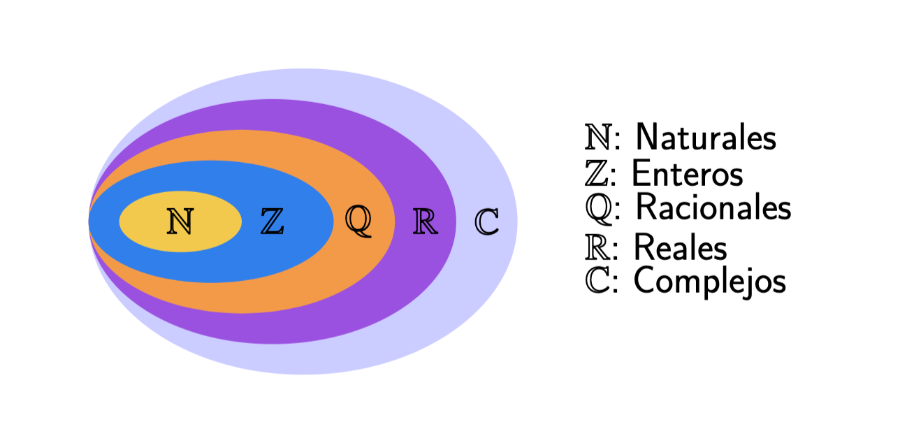
Representación Gráfica de los Conjuntos Numéricos
Pregunta de aplicación práctica - Parte 1
¿En cuál de estas situaciones se utilizan comúnmente los números enteros?
Pregunta de aplicación práctica - Parte 2
¿En cuáles de las siguientes situaciones te verías comúnmente obligado a usar los números irracionales?
Pertenencia a un conjunto: "∈"
El símbolo "∈" se lee como "pertenece a". Se utiliza para expresar que un objeto específico es un miembro de un conjunto. Por ejemplo, podemos escribir cosas como y se lee "uno pertenece a ". De la misma manera, podemos decir que , que o que .
Por otra parte, el símbolo "" se lee como "no pertenece a", y se usa para indicar que un objeto no es parte de un conjunto.Por ejemplo , o
Pregunta de membresía de elementos en conjuntos - Parte 1
¿Cuáles de las siguientes declaraciones son verdaderas?
Pregunta de membresía de elementos en conjuntos - Parte 2
¿Cuáles de las siguientes declaraciones son verdaderas?
Pregunta de membresía de elementos en conjuntos - Parte 3
¿Cuáles de las siguientes declaraciones son verdaderas?
Relación de subconjunto entre conjuntos numéricos
El símbolo de subconjunto es una herramienta crucial en matemáticas para describir la relación entre dos conjuntos. Se representa con "". Cuando decimos que un conjunto A es un subconjunto de un conjunto B, escritos como , estamos afirmando que todos los elementos de A también son elementos de B. Es importante notar que un conjunto siempre es un subconjunto de sí mismo. Por otro lado, también es posible decir que un conjunto no es subconjunto de otro, por ejemplo, que se lee como A no es subconjunto de B, en otras palabras, no todos los elementos de A son también elementos de B.
Ejemplos de Subconjuntos en Conjuntos Numéricos
- Números Naturales en Números Enteros: Los números naturales () son un subconjunto de los números enteros (), ya que cada número natural es también un número entero. Esto se escribe como .
- Números Enteros en Números Racionales: De manera similar, los números enteros son un subconjunto de los números racionales (), ya que cada número entero puede expresarse como una fracción (por ejemplo, el número entero 5 puede expresarse como la fracción ). Esto se representa como .
- Números Racionales en Números Reales: Los números racionales son un subconjunto de los números reales (), ya que cada número racional, siendo una fracción o un decimal finito, también es un número real. Esto se indica con .
Relación de Subcojnunto
¿Cuál de los siguientes conjuntos es un subconjunto de los números reales ()?
Pregunta de relación de subconjuntos numéricos - Parte 1
¿Cuál de los siguientes conjuntos es un subconjunto de los números reales ()?