Punkte berechnen 1
Erste geometrische Bedeutung der Vektoraddition
Aus folgt umgekehrt:
So können in geometrischen Figuren aus gegebenen Punkten weitere Punkte berechnet werden.
Aufgabe 1
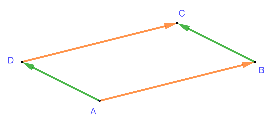
Parallelogramm ABCD: A = (1|-2), B = (5|1), C = (2|2).
a) Konstruiere den Eckpunkt D im folgenden Applet mit Hilfe von Vektoren.
Anleitung:
Verwende den Geogebra-Befehl vektor(_ , _) und die Addition.
b) Berechne den Eckpunkt D auf zwei Arten. 1. Art: wie in Aufgabe 1a. 2. Art: Stelle eine Gleichung für zwei Seitenvektoren auf und löse sie nach D auf.
Aufgabe 2
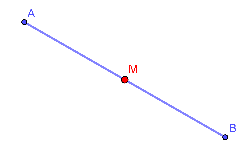
Strecke [AB]: A = (-2|3), B = (5|-1). a) Stelle eine Formel für den Mittelpunkt M der Strecke auf. b) Berechne M. c) Kontrolliere das Ergebnis mit Geogebra.
Zusammenfassung
Gesuchte Punkte können aus gegebenen Punkten berechnet werden, indem man
- an einen gegebenen Punkt einen Pfeil, dessen Koordinaten berechnet werden können, anhängt: oder
- eine Gleichung für Pfeile aufstellt, die den gesuchten und die gegebenen Punkte enthält, und sie nach dem gesuchten Punkt auflöst.