FUNÇÕES EXPONENCIAIS
AUTORES DO TRABALHO: Marina Alves Dos Santos e Wallan Richard Veiga Da Silva
PROFESSORA : NARA BOBKO
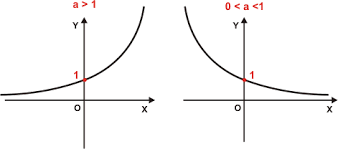
AS FUNÇÕES EXPONENCIAIS SÃO REPRESENTADAS PELA FÓRMULA f(x) = a^x, NO QUAL : - a ∈ - a > 0 DENOMINA-SE FUNÇÃO EXPONENCIAL DE BASE A.A FUNÇÃO EXPONENCIAL PODE SER DECRESCENTE OU CRESCENTE.
A CONDIÇÃO PARA SER CRESCENTE É SE a > 1 E PARA SER DECRESCENTE É a < 1.
ELAS RELACIONAM UMA VARIÁVEL DEPENDENTE A UMA VARIÁVEL INDEPENDENTE, E SUA PRINCIPAL CARACTERÍSTICA É A APARIÇÃO DA VARIÁVEL NO EXPOENTE.
EXEMPLO DE FUNÇÃO EXPONENCIAL
AS FUNÇÕES EXPONENCIAIS POSSUEM ALGUMAS PROPRIEDADES
1ª PROPRIEDADE = Se x = 0, então f(x) = 1.
f(x) = a^x
f(0) = a^0
f(0) = 1
2ª PROPRIEDADE = Se a > 1, então, a função exponencial será crescente.
3ª PROPRIEDADE = Se “a” for menor que 1 e maior que zero, então, a função exponencial será decrescente.
4ª PROPRIEDADE = O gráfico da função exponencial sempre estará localizado acima do eixo x.
Isso acontece porque, por definição, “a” sempre será maior que zero em toda função exponencial. Como “a” é base de uma potência, o resultado dessa potência sempre será maior que zero. Isso significa que, no plano cartesiano, os valores de f(x) correspondentes a y nunca serão negativos, ou seja, nunca ficarão abaixo do eixo x.
Quando a função é decrescente, os valores de y no plano cartesiano aproximam-se de zero sempre que o valor de x aumenta. Caso contrário, a função afasta-se de zero com o aumento de x.
ALGUMAS APLICAÇÕES DAS FUNÇÕES EXPONENCIAIS SÃO :
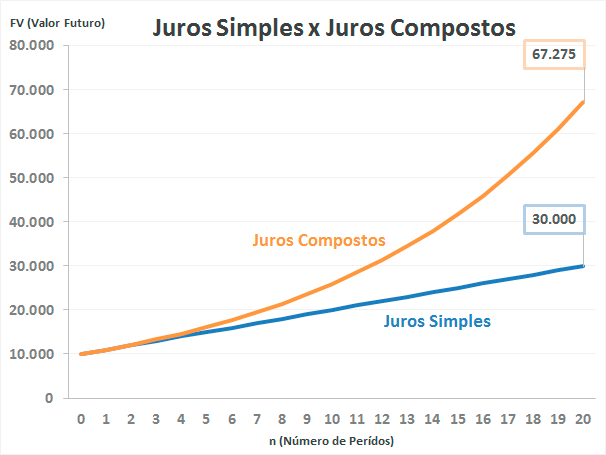
- MATEMÁTICA FINANCEIRA
|-> é utilizada na capitalização de capitais pelo método do juro composto.
- GEOGRAFIA
|-> está relacionada a expressões responsáveis por explicar os crescimentos populacionais.
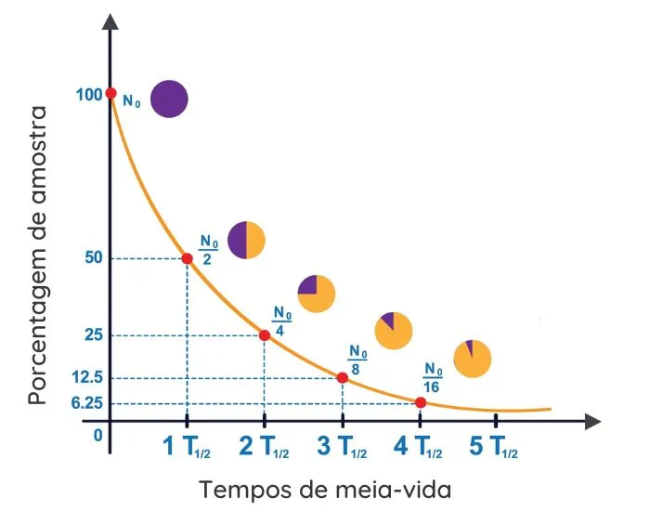
- QUÍMICA
|-> é utilizada em situações envolvendo decaimento radioativo.
- BIOLOGIA
|-> está ligada a desenvolvimento de bactérias em culturas e crescimentos de determinadas plantas.
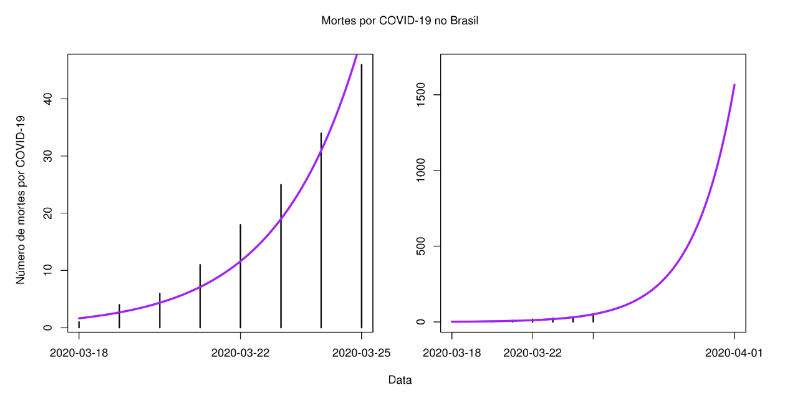
Ela também aparece em outras áreas como: Economia, Engenharia, Astronomia, Física e Medicina.
APLICAÇÕES REAIS DETALHADAS DA FUNÇÃO EXPONENCIAL
Matemática Financeira
Um dos exemplos mais comuns das funções exponenciais, e que é muito frequente em finanças, é o cálculo do rendimento de uma quantia em dinheiro aplicado em um banco que paga uma certa taxa percentual durante determinado tempo, com o Montante (capital + juro) retirado no fim do contrato.
M = C . ( 1 + i )^n no qual C representa o Capital aplicado, i é a taxa percentual escrita como fração decimal, n é o número de períodos de tempo que demorou a aplicação, lembrando que taxa i e número de períodos de tempo não devem se referir à mesma unidade de tempo.
EXEMPLO DE COMO A MATEMÁTICA FINANCEIRA PODE UTILIZAR A FUNÇÃO EXPONENCIAL
Modelo de Malthus
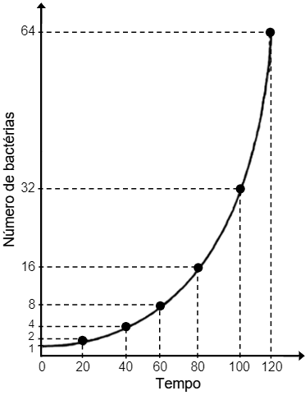
Um dos primeiros modelos matemáticos elaborados para descrever o crescimento de uma população foi o modelo de Malthus. Este modelo parte do pressuposto de que o número de indivíduos em um determinado instante de tempo t é proporcional ao quanto a população aumentou (ou diminuiu) do instante anterior para o atual. Por trás deste pressuposto está uma hipótese importante: as condições para o desenvolvimento desta população são ideais, ou seja, há alimento suficiente para todos os indivíduos, não existem limitações de espaço, não ocorrem situações que possam causar danos à população, etc.
Neste caso, a função exponencial P(t)=P0·e(k·t) nos informa a quantidade de bactérias no instante t, onde P0 é quantidade inicial de bactérias e k é uma constante dada pela taxa de natalidade menos a taxa de mortalidade dos indivíduos, em geral determinada empiricamente.
UMA REPRESENTAÇÃO MAIS SIMPLES DO MODELO DE MALTHUS, NO QUAL ALÉM DE TEREM CONDIÇÕES IDEAIS, AS BACTÉRIAS NÃO MORREM AO PASSAR DO TEMPO :
EXEMPLIFIQUE UMA APLICAÇÃO DA FUNÇÃO EXPONENCIAL
QUAL É O FORMATO DO GRÁFICO DA FUNÇÃO EXPONENCIAL ?
DADA UMA FUNÇÃO COM A LEI DE FORMAÇÃO F(x) = ax, EM QUE a É UM NÚMERO POSITIVO DIFERENTE DE 1, JULGUE AS AFIRMATIVAS A SEGUIR : | ESSA FUNÇÃO SERÁ CRESCENTE SE a FOR POSITIVO. || SE x = 0, ENTÃO F(x) = 1. ||| ESSA É UMA FUNÇÃO EXPONENCIAL. ESCREVA AS AFIRMATIVAS CORRETAS.