Methode der kleinsten Fehlerquadrate
Die Methode der kleinsten Quadrate (kurz KQ-Methode) ist das mathematische Standardverfahren zur Ausgleichungsrechnung. Dabei wird zu einer Datenpunktwolke eine Kurve gesucht, die möglichst nahe an den Datenpunkten verläuft (wikipedia).
Messwerte P,Q,R im Koordinatensystem. Gemessen werden die Abstände (Residuen) Messwert (x,y) zur Ausgleichsgeraden g(x) die möglichst "gut" an die Punkte angenähert werden soll.
Die Summe der Residuenquadrate ri=(g(xi)-yi)2 soll minimiert werden.
ri=(g(xi)-yi)2
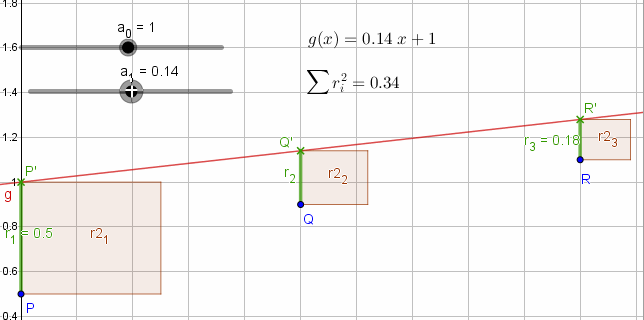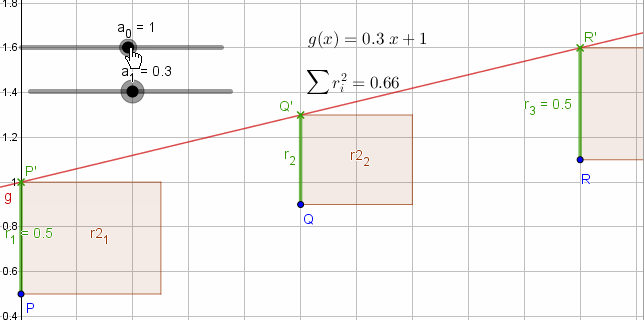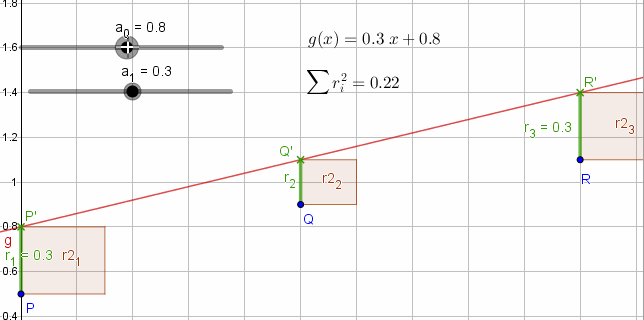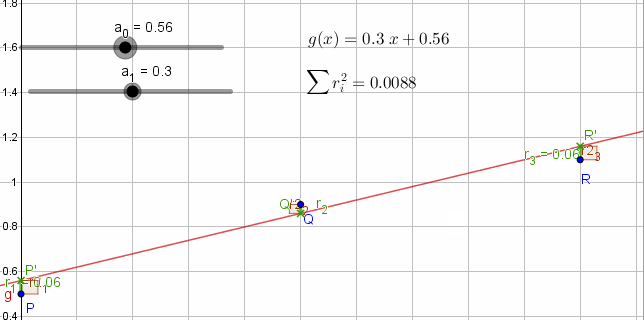
Minimiere Residuenquadrate durch partielle Ableitung nach den Funktionskoeffizienten dQ={ , }. Die Lösung dieses LGS liefert die Koeffizienten ai der gesuchten Funktion.
Ab Zeile 18 entwickle ich die Normalengleichung. Durch Einsetzen der gegebenen Punkte in die allgemeine Funktionengleichung erhalte ich die Koeffizientenmatrix [f(Xi)]=A und für A ai = b.
Die Matrixversion der Ableitungen dQ stellt sich als Normalengleichung dar und damit berechne ich ebenfalls die Koeffizienten der Regressionsfunktion.
Die Normalengleichung löse ich durch die Inverse .
Allgemeine Version für Polynomregression
Version Exponential-Power-Regression-Model
Ändern Datenmodell: X,Y (Werte Listen) mit neuen Daten belegen!
Allgemeine Version für Polynomregression
Version Exponential-Power-Regression-Model
Ändern Datenmodell: X,Y (Werte Listen) mit neuen Daten belegen!Einfache Regression für eine Gerade
AlgebraView (CAS mit List-Index Element())
XY: {(10, 1), (25, 7 / 5), (45, 5 / 2), (60, 3)}
X: x(XY)
Y: y(XY)
n: length(X)
X_m:mean(X)
Y_m:mean(Y)
a_1: Sum((X(i)-X_m)(Y(i) -Y_m) ,i,1,n)/sum((X(i)-X_m)^2,i,1,n)
f(x):=(Y_m - a_1 X_m) + a_1 x
CorrelationCoefficient(XY)
r=Sum((X(i)-X_m)(Y(i)-Y_m),i,1,n)/sqrt(Sum((X(i)-X_m)^2,i,1,n)Sum((Y(i)-Y_m)^2,i,1,n))