Primeira relação de desigualdade
Teorema
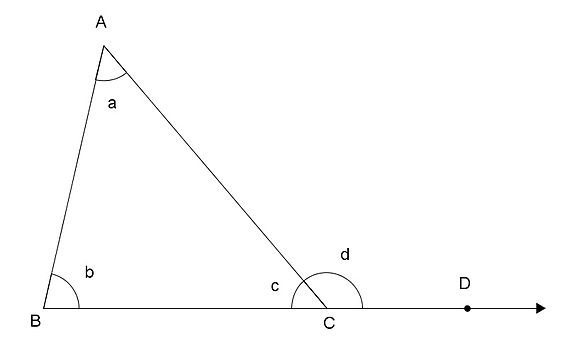
Um ângulo externo de um triângulo é o resultado da soma dos dois ângulos internos não-adjacentes.
Demonstração
Na figura acima, observamos que os ângulos 
, 
, 
são os ângulos internos do triângulo 
e temos que 
é um ângulo externo.
Assim, um ângulo externo de um triângulo é o ângulo formado pelo prolongamento de um lado e o lado adjacente. O ângulo externo é suplementar ao interno adjacente.
A demonstração mais trivial passa pelo fato de que o ângulo externo é suplementar ao ângulo interno adjacente. Partindo disso, temos que 
.
Em todo triângulo temos que a soma de todos os ângulo internos é igual a dois ângulos retos, ou um ângulo raso, assim, temos que 
. Podemos isolar o 
, de modo a obter 
Então aplicaremos essa última relação em e teremos que :
Assim, temos que todo ângulo externo é igual à soma dos ângulos internos não adjacentes. E também temos que 
e 
pois d é a soma de a e b.
, , são os ângulos internos do triângulo e temos que é um ângulo externo.
Assim, um ângulo externo de um triângulo é o ângulo formado pelo prolongamento de um lado e o lado adjacente. O ângulo externo é suplementar ao interno adjacente.
A demonstração mais trivial passa pelo fato de que o ângulo externo é suplementar ao ângulo interno adjacente. Partindo disso, temos que .
Em todo triângulo temos que a soma de todos os ângulo internos é igual a dois ângulos retos, ou um ângulo raso, assim, temos que . Podemos isolar o , de modo a obter
Então aplicaremos essa última relação em e teremos que :
Assim, temos que todo ângulo externo é igual à soma dos ângulos internos não adjacentes. E também temos que e pois d é a soma de a e b.