10. ระบบพีชคณิตคอมพิวเตอร์ (1) (Version 2)
ชื่อ - สกุล รหัสนิสิต 3 ตัวท้าย
เช่น นายวีริศ กิตติวรากูล 500
จุดประสงค์การเรียนรู้
เพื่อให้นิสิตครูสามารถใช้ระบบพีชคณิตคอมพิวเตอร์ในการแก้ปัญหาทางคณิตศาสตร์ได้
1. การคำนวณหาผลลัพธ์พื้นฐานของระบบพีชคณิตคอมพิวเตอร์
การดำเนินการและฟังก์ชันในการคำนวณที่ควรทราบ มีดังนี้
1) การดำเนินการบวก ลบ คูณ และหาร ให้ใช้แป้นพิมพ์ +, -, * และ / ในการ input ตามลำดับ
2) การหา ห.ร.ม. ของจำนวน n จำนวน สามารถ input ด้วยคำสั่ง GCD(<จำนวนที่ 1>,<จำนวนที่ 2>, ...,<จำนวนที่ n>)
3) การหา ค.ร.น. ของจำนวน n จำนวน สามารถ input ด้วยคำสั่ง LCM(<จำนวนที่ 1>,<จำนวนที่ 2>, ...,<จำนวนที่ n>)
4) การตรวจสอบจำนวนเฉพาะ สามารถ input ด้วยคำสั่ง isprime(<จำนวน>)
5) การดำเนินการยกกำลัง ให้ใช้แป้นพิมพ์ ^ ในการ input
6) การหากรณฑ์ที่สอง สามารถ input ด้วยคำสั่งในรูป sqrt(<จำนวน>)
7) การหารากที่ n สามารถ input ด้วยคำสั่งในรูป nroot(<จำนวน>,<รากที่ n>)
8) การหาค่าสัมบูรณ์ สามารถ input ด้วยคำสั่งในรูป abs(<จำนวน>)
9) การหาค่าของฟังก์ชันลอการิทึม สามารถ input ด้วยคำสั่งดังต่อไปนี้
- input ด้วยคำสั่ง log(<ฐานของลอการิทึม>,<จำนวน>)
- input ด้วยคำสั่ง ln(<จำนวน>)
หมายเหตุ : ค่าคงตัว e ใน CAS ให้กดแป้นพิมพ์ Alt + e เนื่องจากกรณีที่ผู้ใช้พิมพ์ e โปรแกรมจะมองเป็นตัวแปรตัวแปรหนึ่ง
10) การหาค่าของฟังก์ชันตรีโกณมิติ สามารถ input ด้วยคำสั่งดังต่อไปนี้
- input ด้วยคำสั่ง sin()
- input ด้วยคำสั่ง cos()
- input ด้วยคำสั่ง tan()
- input ด้วยคำสั่ง cosec() (ใช้ csc แทน cosec ได้)
- input ด้วยคำสั่ง sec()
- input ด้วยคำสั่ง cot()
หมายเหตุ : - ค่าคงตัว ให้พิมพ์ว่า pi
- หากต้องการคำนวณหน่วยองศา ให้ใช้ Virtual Keyboard ในการใส่สัญลักษณ์ ประกอบ เช่น sin(30)
11) การหาค่าของตัวผกผันของฟังก์ชันตรีโกณมิติ สามารถ input ด้วยคำสั่งต่อไปนี้
- input ด้วยคำสั่ง arcsin(<จำนวน>) (ใช้ asin แทน arcsin ได้)
- input ด้วยคำสั่ง arccos(<จำนวน>) (ใช้ acos แทน arccos ได้)
- input ด้วยคำสั่ง arctan(<จำนวน>) (ใช้ atan แทน arctan ได้)
12) การกำหนดเวกเตอร์ หรือ สามารถ input ด้วยคำสั่ง vector(<ค่า x>,<ค่า y>) หรือ vector(<ค่า x>,<ค่า y>,<ค่า z>)
13) การกำหนดจำนวนเชิงซ้อน สัญลักษณ์ของส่วนจินตภาพ i ให้กดแป้นพิมพ์ Alt + i
14) การหาค่าของแฟคทอเรียล สามารถพิมพ์สัญลักษณ์ "!" หลังจำนวนได้เลย เช่น 5!
จงใช้ Applet ระบบพีชคณิตคอมพิวเตอร์ หรือ Algebra แสดงการคำนวณในแต่ละแถวดังต่อไปนี้
Row 1.
Row 2.
Row 3.
Row 4.
Row 5.
ให้พิมพ์แสดงการคำนวณในแต่ละแถวให้ถูกต้อง
2. Symbolic Evaluation และ Numeric Evaluation
Symbolic Evaluation
- เป็นการคำนวณผลลัพธ์ให้แสดงออกมาอยู่ในรูปสัญลักษณ์ (คำตอบเป็นเศษส่วน หรืออยู่ในเครื่องหมายกรณฑ์)
- สามารถปรับคำตอบให้แสดงผลแบบ Symbolic Evaluation โดยการคลิกปุ่ม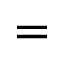 
ใน Row ที่ต้องการให้เปลี่ยนการแสดงผล
Numeric Evaluation
- เป็นการคำนวณผลลัพธ์ให้แสดงออกมาอยู่ในรูปตัวเลขเท่านั้น (คำตอบเป็นทศนิยม ไม่มีสัญลักษณ์เศษส่วน หรือเครื่องหมายกรณฑ์)
- สามารถปรับคำตอบให้แสดงผลแบบ Numeric Evaluation โดยการคลิกปุ่ม 
ใน Row ที่ต้องการให้เปลี่ยนการแสดงผล
การปรับการแสดงผลจำนวนตำแหน่งของทศนิยม
1) เปิดหน้าต่าง Settings
2) ปรับ Rounding ให้เป็นจำนวนตำแหน่งของทศนิยมตามที่ต้องการ
ใน Row ที่ต้องการให้เปลี่ยนการแสดงผล
Numeric Evaluation
- เป็นการคำนวณผลลัพธ์ให้แสดงออกมาอยู่ในรูปตัวเลขเท่านั้น (คำตอบเป็นทศนิยม ไม่มีสัญลักษณ์เศษส่วน หรือเครื่องหมายกรณฑ์)
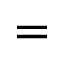- สามารถปรับคำตอบให้แสดงผลแบบ Numeric Evaluation โดยการคลิกปุ่ม ใน Row ที่ต้องการให้เปลี่ยนการแสดงผล
การปรับการแสดงผลจำนวนตำแหน่งของทศนิยม
1) เปิดหน้าต่าง Settings
2) ปรับ Rounding ให้เป็นจำนวนตำแหน่งของทศนิยมตามที่ต้องการจงใช้ระบบพีชคณิตคอมพิวเตอร์
1) แสดงค่าประมาณของ ถึงทศนิยมตำแหน่งที่ 15 ใน Row 1
2) แสดง 0.5 ในรูปของเศษส่วน (แสดงผลลัพธ์เป็น ) ใน Row 2
3. การกำหนดค่าของตัวแปร
การกำหนดค่าของตัวแปร
ถ้าต้องการกำหนดตัวแปร a ให้มีค่าเป็น 1 ให้ป้อน input เป็น a := 1 แล้วกด Enter จะทำให้ระบบจำว่า a มีค่าเท่ากับ 1
การยกเลิกการกำหนดค่าของตัวแปร
ให้ลบ Row ที่มีการกำหนดค่า a ออก จะทำให้ a กลับไปเป็นตัวแปรเหมือนเดิม
4. ระบบพีชคณิตคอมพิวเตอร์กับตัวแปรชนิดจำนวนและบูลีน
1) การแก้สมการ โดยใช้ฟังก์ชัน solve
เช่น Input: solve(x+2=5)
ผลลัพธ์: {x=3}
Input: solve(a^2+3a+2=0,a)
ผลลัพธ์: {a=-2, a=-1}
2) การจัดนิพจน์ให้อยู่ในรูปอย่างง่าย โดยใช้ฟังก์ชัน simplify หรือ expand
เช่น Input: simplify((x+1)^2))
ผลลัพธ์:
Input: expand(1/sqrt(2))
ผลลัพธ์:
3) การแยกตัวประกอบของจำนวนเต็ม หรือพหุนาม สามารถ input โดยใช้ฟังก์ชัน factor
เช่น Input: factor(10}
ผลลัพธ์:
Input: factor(x^2-5x+6}
ผลลัพธ์: (x-3)(x-2)
4) ตัวดำเนินการทางตรรกศาสตร์ ให้ใช้ Virtual Keyboard ดังนี้
หมายถึง "และ"
หมายถึง "หรือ"
หมายถึง "ถ้า ... แล้ว"
เช่น Input: true false
ผลลัพธ์: false
5) การกำหนดฟังก์ชัน
เช่น Input: f(x):=2x+1
ผลลัพธ์: กำหนดฟังก์ชัน f เป็น f(x)=2x+1
Input: f(x):=if(x<0,-1,1)
ผลลัพธ์: กำหนดฟังก์ชัน f โดยนิยามดังนี้
6) การหาลิมิตของฟังก์ชัน
1) limit(<ฟังก์ชัน>,<ค่าที่เข้าใกล้>) /* สำหรับการหาลิมิต */
2) limitbelow(<ฟังก์ชัน>,<ค่าที่เข้าใกล้>) /* สำหรับการหาลิมิตซ้าย */
3) limitabove(<ฟังก์ชัน>,<ค่าที่เข้าใกล้>) /* สำหรับการหาลิมิตขวา */
*7) การหาอนุพันธ์ของฟังก์ชัน โดยใช้ฟังก์ชัน derivative ซึ่ง input ในรูป
- derivative(<ฟังก์ชัน>,<ตัวแปร>) หรือ กรณีที่หาอนุพันธ์อันดับสูง ให้แทนค่า input เป็น
- derivative(<ฟังก์ชัน>,<ตัวแปร>,<อันดับของอนุพันธ์>)
เช่น
Input: derivative(3x^4-2/3x^3+5x-1)
ผลลัพธ์:
Input: derivative(x^2-1,x,2)
ผลลัพธ์: 2
ตัวอย่างการหาอนนุพันธ์เมื่อมีการแทนค่าตัวแปร x
Input: g(x)=derivative(x^2,x)
g(1)
ผลลัพธ์: 2
*8) การหาปริพันธ์ของฟังก์ชัน โดยใช้ฟังก์ชัน integral ซึ่ง input ในรูป
- integral(<ฟังก์ชัน>,<ตัวแปร>) /* กรณีหาปริพันธ์ไม่จำกัดเขต */
- integral(<ฟังก์ชัน>,<ตัวแปร>,<ขอบล่าง>,<ขอบบน>) /* กรณีหาปริพันธ์จำกัดเขต */
เช่น Input: integral(sqrt(x),x)
ผลลัพธ์:
Input: integral(x,x,x=0,x=1)
ผลลัพธ์:
* หมายเหตุ การใส่ฟังก์ชันในการหาอนุพันธ์ให้เขียนเฉพาะส่วนของตัวแปร x เท่านั้น เช่น ต้องการหาอนุพันธ์ของ ให้ input ฟังก์ชันเป็น เท่านั้น
จงใช้ระบบพีชคณิตคอมพิวเตอร์หาคำตอบในแต่ละต่อไปนี้
Row 1. แก้สมการ
Row 2. แยกตัวประกอบของพหุนาม
Row 3. หาค่าความจริงของประพจน์
(เมื่อ T แทนประพจน์ที่มีค่าความจริงเป็นจริง และ F แทนประพจน์ที่มีค่าความจริงเป็นเท็จ)
Row 4. หาพื้นที่ที่ปิดล้อมด้วยเส้นโค้ง กับแกน X จาก x = 1 ถึง x = 2
Row 5. หาอนุพันธ์อันดับสองของ เมื่อ x = 0