Агуулга
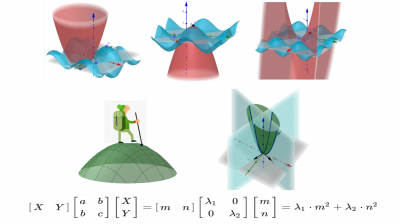
Interpretation of the Eigenvalues of the Hessian Matrix
Identifying a stable point as a maximum, minimum, or saddle point in a multivariable case. Visualizing the eigenvalues and eigenvectors of the Hessian matrix.
You should know before you read:
1. High school calculus. It's better if you know some multivariable calculus too, but it's okay if you don't.
2. Basic linear algebra knowledge (having watched 3Blue1Brown's linear algebra series would be enough), particularly understanding the meaning of eigenvectors, eigenvalues, and the change of basis in matrices. But no stress, I'll still go through these important subjects in the passage.
The mini geogebra programs in this project are all interactive, both their algebraic columns and their graph areas. Feel free to play around with them!