Chebyshev Amoeba (Alias: Octagon wheel)
Conceptional animation
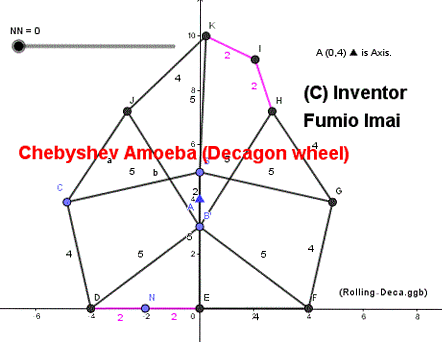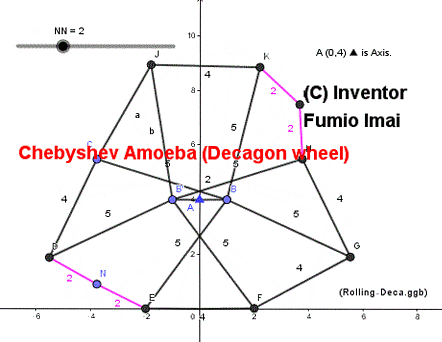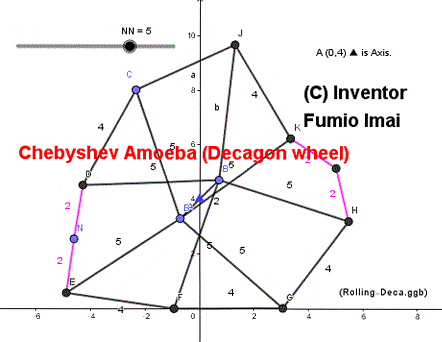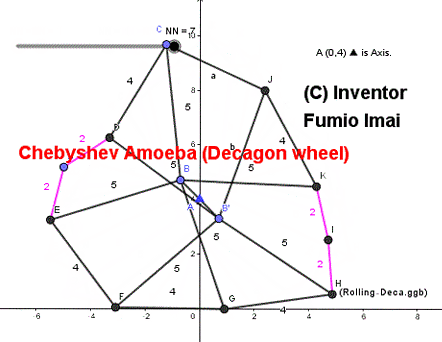
■ Chebyshev Amoeba ( = Discrete wheel )
I'm an inventor of this, from a inventor's privilege, I would like propose to name this figure "Chebyshev Amoeba" like as "Reuleaux triangle (wikipedia)".
This apparatus is related to the non-punctured tire "Run-flat tire" (wikipedia), too.
Its rough shape is Octagon. and sometimes, it becomes Nanogon or Decagon.
This amoeba's body center height is constant when it is set on the ground and is pushed by gravity.
So, it has wheel property.
I think if Reuleaux triangle is famous, if so, Chebyshev Amoeba should be become more famous than Reuleaux triangle, because it is useful in real-life, perhaps.
■ Simple algorithm.
This is only a Chebyshev Linkage loop.
Adjacent Chebyshev Linkage units.
(More precise definition: This is an application of Chebyshev-Imai Pantograph.)
Merit than ordinary Continuous track (wikipedia).
1. not noisy.
2. cheap
3. high speed (?) light weight (?)
4. maintenance is easy (?).
ex. Σ (Flat tire-parts) --- 8 edges. One parts individual resale is OK.
5. New-typed Wheelchair etc. or tractor, exercise bicycle, ...
■ Easy implementation sample (Two pedals case)
In above picture, I supposed Chebyshev Linkage Unit is 4, 5, 2, 5 length bars.
Outer edge length are 4+4+4+4+4+4+4+about 3.5. (total 7×4 + about 3.5)
[ 7×4 + 3.5 = 31.5 ---- ≒ 10π why? , I wonder. ]
CDKM Chebyshev-unit is the remainder of dividing by 4 length edge.
The edge AB and KM is variable length (= about 3.5).
And if AB and KM is on the ground case, its length must be 4.
( 2 + 2 bent bars 凸 structure, if touching the ground, it becomes 180° angle. )
( ∠KUK' = 90°, ∠MUM' = 90°, so keeping 凸 is made by ∠K'UM' ≧ 0 .
To prevent minus angle, prepare the stopper sheet between K' and M'. )
Other all edges are constant 4.
------
Concept is above. --- But, above picture is bad crank system in pedal part. ∵ 2 pedals system.
(Crank is complex. bad robustness.)
/// I recommend the below picture implementation. //// ☜ NO KID !!!
■ Pedal C only one crank is available. (One pedal case)
More easy implementation.
See below picture. [ A (0, 4) ▲ is Crank axis. ]
Rolling-Amoeba.
Tip: This method makes simple crank, but total necessary bars increases.
i.e. + 8 bars.
--- This is very clever TRICK (!?) --- Crank center shift trick. number of edges are the even. It's key.
(We can change 2 pedals system into equivalent 1 pedal system easily. )
∵ Already small clone was gotten, so large clone information can get from it.
■ Thick-soled shoes method is bad.
From the simulation test figure, the thick-soled shoes method is worse than the bent-bar method.
(thick-soled shoes method occurs the hiccup.)
So, you must adopt the bent-bar method for 4th and 8th edges.
凸 bent bar. ---- This is total nonagon.
( If one bent-bar edge touches the ground, this bent-bar becomes straight
and, another bent-bar forces to be bent. So, bent-bar edges is needed two or more. )
But in one pedal method case, other method is needed.
→ Answer is in below "One pedal case:" Fig.
Dividing 8 edge bars into 2 groups. --- i.e. One group has 4 edge member.
Cyan color bars is the answer. Twice bent-bars are needed than 2 pedals case.
( i.e. IF Cyan bars touch the ground, the overlapping gap C'1C'5 becomes 0, and opposite side gap becomes non-0. ) ------ Instead of this, Lime color bent-bar is OK too.
[ In implementation view sense, Lime method is better than Cyan method, of course.
Comment: There is a case which Nodes C'5/ C'1 are out side of lime bar (WC'2 or WT),
but, when node W is near the ground, ∠TWC'2 is always obtuse angle,
so this outside-node problem is not mind. ]
Please consider more elegant implementation.
■ Related wheel
cf1. Chebyshev couple N=2 (Chebyshev couple application)
cf2. Cassini Wheel (N=4 4R Virtual Wheel)
■ Property of Chebyshev linkage
Axis trace has next property.
① ≒ constant height : 4.00 to 4.00975 ,, So, almost straight line.
② ≒ constant velocity : (Pedal angle [45°× N], move distance)
(N, distance) N=0,1,...,8 result:
(0,0), (1, 0.9445), (2, 2), (3, 3.0209), (4,4), (5, 4.9721), (6,6), (7, 7.0555), (8, 8)
--- So, almost constant velocity.
■ Last result
Next picture indicates the bar combination form.
Simple it is!
---- Please enjoy.
cf. Bicycle wheel (wikipedia) -- near?
corresponding to Bicycle wheel
2 (pedal part) is hub
5 is spark
4 is lim
■ Chebyshev-Imai Pantograph
Chebyshev-Imai Pantograph ia a 9 bars linkage.
Its top head axis position keeps horizontally or more upper area.
Chebyshev Amoeba last model is composed by 4 Chebyshev-Imai Pantographs.
So, last model logic trueness is proved by mathematically.
cf. Pantograph (transport) (wikipedia)
■ No gap edge length analytical estimation
Chebyshev straight line mechanism ratio has a family group value.
Chebyshev's Lambda Mechanism Linkage length ratio = 1 : 2 : 2.5 ------ This ratio is basic. (wikipedia)
Generalization = 1 : bb : 0.5 sqrt [ (bb2+1)(2bb+1) ] ------- ratio eq.
cf. Musashikoganei Square Wheel link ← equation proof page.
( pedal angle span 180°, height is almost constant [at least 0°, 90°, 180° 's height is exact equal ]. )
From this equation, gap zero ratio was
original Chebyshev 4, 5, 2, 5 ⇒ Amoeba Chebyshev
4.309198068172,
5.473214075856918,
2,
5.473214075856918
These ratio value provides almost straight line.
And, This ratio Chebyshev Amoeba has no-gap edge.
8th bar length order = 4.3091980681723 to 4.3091980681724 [≒ 4.31] --- almost constant (good property)
[+ 0.0000000000001/4.3 err order, increase monotone]
Center axis height order = 4.47085 to 4.47694 --- under 0.14% [+ 0.00609/ 4.4 err order]
( This height err order is better than 4/5/2/5 ratio original Chebyshev.
∵ 4.00 to 4.00975 order. --- i.e. 0.24% [+ 0.00975/ 4.0 err order] )
In real life, this order of errors is no harm.
Tip: bar LA length is almost constant, but in order to absorb the backlash I recommend to use bent-bar of LA. (???) ---- it may be unnecessary (?). --- In one pedal system, it occurs the problem.
(If 2 points are fixed, between bent-bars will be fixed, but 3 bent-bar is not fixed. so, bent-bar is bad. )
Here, No needed consideration for opposite side bent-bar.
Even if LA length were set constant, in one pedal system case, DL long bar doesn't exist (∵ Node D is none), so the backlash doesn't occur. (?) Is this true?
Connect LA loosely. ---- This is answer. ex. old (●) → new ( ● ) linkage connector with cushion.
See next picture.
( if AB length > 4 and AB is on the ground;
pedal angle 0° [CD is vertical] : but center x(E) > 0 , ∠DAB is acute. Node L is not on the ground.
∠LAB = 177.41° (< 180°). So, 180°-177.41° = 2.59° down & up seesaw play happens.
1-cos(2.59°) = 0.13% Axis gap ratio. --- this err ratio is the same degree linearity err order 0.15%.
So, we can neglect its err.
So, frequent Hiccup will occur. but this hiccup is negligible.
∵ Even if pedal angle ≒ 0° or 180°, in short time height is kept. so safety. y(E) is almost constant is kept. )
Tip: This method, all edge length are the same, but negligible hiccups occurs at every edge end.
(i.e. Outer wheel 360°, 8 times hiccups happen. But, previous method, Wheel 360°, 1 times hiccup
no hiccup [2 times gap adjustments happen].)
(To reduce the hiccups and its damages, many/ various methods are there. Please ponder.)
177° bent-edge is corresponded to 3° radius angle, This is a 320°/3° = 120 polygon which simulates a circle.
120 polygon has 177° edge, it may hurt the ground. --- but, negligible. (?)
( Logically, it doesn't not hurt the ground. ∵ pedal angle (180+ε)° keeps the same height. ε is small. )
Comment: If needed, please wear Japanese Geta (= wood sandal).
So, (4.309198..., 5.473214..., 2) ratio and ( 4.082845..., 5.167407..., 2) ratio both are feasible.
Chebyshev Amoeba (Oct-177)
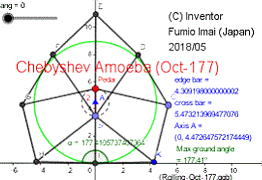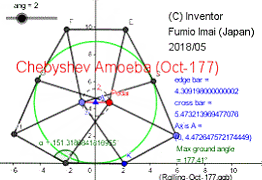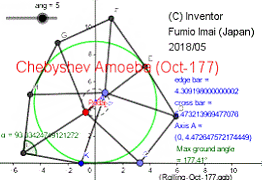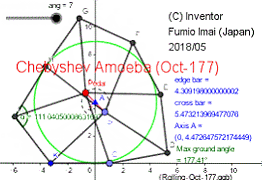
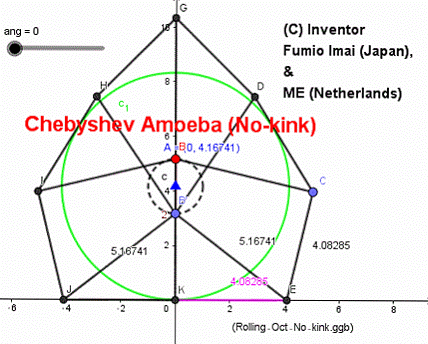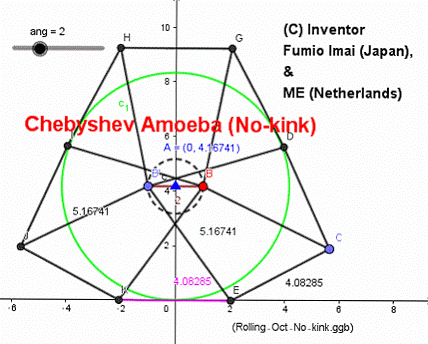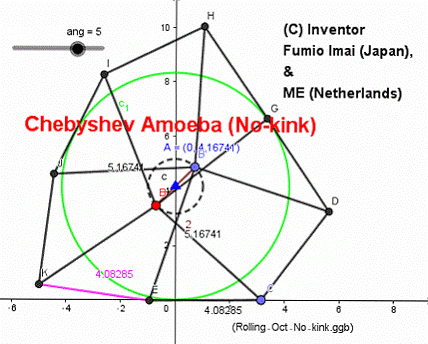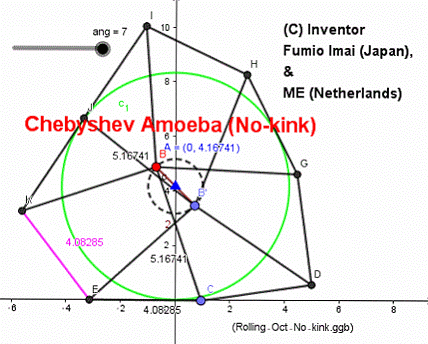
Tue Apr 17, 2018
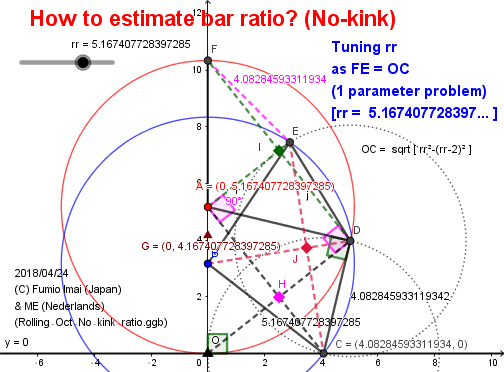
Mr. "ME" (Nederlands) suggested me a below ratio.
-- Gap length (KE segment) ≒ constant --
Inner radius: 1 (or axle diameter 2)
Edge-length: e = 4.082845933119... = √[r2-(r-2)2] = 2 √(r-1)
Radial-length: r = 5.167407728397...
-----
axle trace is almost line.
height: -- err order is < 0.015/4 (= 0.37%)
min 4.16741 (x=0)
min 4.17754 (x=2)
max 4.18217 (x=1)
[ Original Chebyshev linkage 2:4:5:5 bars
height is from 4.0 to 4.00975 ,
err order is < 0.00975/4 (= 0.24%) ]
Test result under Option "Rounding": 15 Decimal Places
In another angle amoeba shape, this pink segment length changes a bit (= negligible).
4.082845933118707 max
4.082845933118416 min
0.000000000000291 err order
So, bent-bar mechanism can be negligible.
This err value is too too small (= accurate).
Perhaps, this edge length is independent to any angle, mathematically.
----
Analytical calculation. --- r tuning.
A= (0, r), B = (0, r-2), F = (0, 2r), O = (0, 0)
C = (sqrt(r2-(r-2)2), 0) = (2 sqrt(r-1), 0)
D = (4r2sqrt(r-1)/(r2+4r-4), 8r(r-1)/(r2+4r-4) )
x(E) = [-2 (r-2) t -2 sqrt(r-1) (t2 -1) ] / [t2 +1]
y(E) = ( r3 + 2r2 +4r -8) / {r2[t2 +1] }
here,
t = (-r3 + 6r2 +4r -8) / [4r2 sqrt(r-1)]
t2 +1 = (r6 +4r5 + 12r4 +64r3 -80r2 -64r +64) / (16r5 -16r4)
What a tremendous equation it is!
----
on 2018/04/27
Japanese Mr. Rascal says ,
r is the next quintic equation's root.
x5-2x4-16x3-16x+32 = 0
(or s=2x, s5-s4-4s3-s+1 = 0 is equivalent.)
He indicates 50 decimals value.
r = 5.16740772839728595747372780506339609865810833312219...
e = 4.08284593311934118466290274562471952834199482221455...
■ No-kink r equation
vector AE = { [-2 (r-2) t -2 sqrt(r-1) (t2 -1) ] / [t2+1], ( r3 + 2r2+4r -8) / {r2[t2 +1] } -r }
vector AC =(2 sqrt(r-1), -r)
AE ⊥ AC ---- So, inner product = 0
[-2 (r-2) t -2 sqrt(r-1) (t2 -1) ] * [2 sqrt(r-1)]/ [t2+1] - r * ( r3 + 2r2 +4r -8) / {r2[t2+1] } +r2 =0
[-2 (r-2) t -2 sqrt(r-1) (t2 -1) ] * [2 sqrt(r-1)] -(1/r)* ( r3 + 2r2 +4r -8) +r2*[t2+1] = 0
(-4)*[ (r-2) *sqrt(r-1)*t + (r-1) (t2 -1)] - [(r3+ 2r2 +4r -8) -r3*(t2+1)]/r = 0
(-4)r * [ (r-2) *sqrt(r-1)*t + (r-1) (t2 -1)] - [(r3 + 2r2+4r -8) - r3*(t2+1)] = 0
(-4)r*[(r-2) *sqrt(r-1)* (-r3 + 6r2 +4r -8) / [4r2 sqrt(r-1)] + (r-1) (t2 -1)] - [(r3 + 2r2 +4r -8) - r3*(t2+1)] = 0
[(-1/r)*(r-2) * (-r3 + 6r2 +4r -8) +(-4r) (r-1) (t2 -1)] - [(r3 + 2r2+4r -8) - r3*(t2+1)] = 0
Multiply (-r) then,
(r-2) * (-r3 + 6r2 +4r -8) + 4r2(r-1) (t2 -1) + r [(r3 + 2r2 +4r -8) - r3*(t2+1)] = 0
-r4+6r3+4r2-8r +2r3-12r2-8r+16 + [4r3-4r2]t2 -4r3+4r2 + r4+2r3+4r2-8r
-r24t2
-r4 = 0
-r4+6r3
-24r +16 +[-r4+4r3-4r2]t2 = 0
-r4+6r3 -24r +16 +[-r4+4r3-4r2] (t2+1) -[-r4+4r3-4r2] = 0
2r3 +4r2 -24r +16 +[-r4+4r3-4r2] (t2+1) = 0
[2r3 +4r2 -24r +16] +[-r4+4r3-4r2] *(r6 +4r5 + 12r4 +64r3 -80r2 -64r +64) / (16r5 -16r4) = 0
[2r3 +4r2 -24r +16] (16r5 -16r4) +[-r4+4r3-4r2] *(r6 +4r5 + 12r4 +64r3 -80r2 -64r +64) = 0
Both side divide by r2
16*[2r3 +4r2 -24r+16] (r3-r2) +[-r2+4r-4]*(r6 +4r5 + 12r4 +64r3 -80r2 -64r +64) = 0
32r6 +64r5 -384r4 +256r3
-32r5 -64r4 +384r3 -256r2 +
-r8-4r7-12r6 -64r5 +80r4 +64r3 -64r2
4r7 16r6 48r5+256r4 -320r3 -256r2 +256r
-4r6 -16r5 -48r4 -256r3 +320r2 +256r -256 = 0
-r8 +32r6 -160r4 +128r3 -256r2 +512r -256 =0
-------
x8 -32x6 +160x4-128x3+256x2-512x+256
=(x-2)(x2+4x-4) (x5-2x4-16x3-16x+32) = 0 ----- This is the answer.
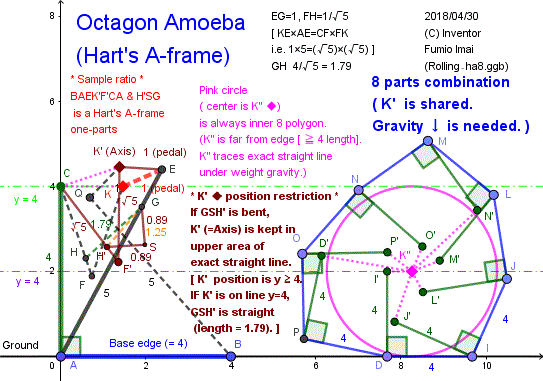
■ Exact straight line Axis trace apparatus.
【 Modification of Chebyshev Amoeba (no-kink) .】
If replace the component from Chebyshev linkage to Hart's A-frame,
we can make exact straight line axis Octagon wheel easily.
Keypoint:
GSH' is a bent bar, this is great.
Please ponder its reason.
Tip:
In Chebyshev linkage, next is true.
AE=a, EK=b, CK=c, CA=a-b, ∠AEK= Θ
If K is on the line,
(AK)2= (a-b)2+c2= a2+b2-2ab+c2
(AK)2= a2+b2-2ab*cos[Θ]
so,
c2= 2ab(1-cos[Θ])= 2ab(2sin2[Θ/2])
so,
c= 2(√[ab]) sin[Θ/2] (--- This is ∽ KG)
so, length property
CK ∽ KG ---- This is big property.