3. Nullstellen und Faktorisieren - Vielfachheit von Nullstellen
Du kennst bereits den Zusammenhang zwischen der Anzahl der Nullstellen und dem Grad der Polynomfunktion.
Hier eine kleine Aufwärmung:

Lies dir die obigen Aussagen durch und veranschauliche sie dir eventuell mit einer Skizze. Entscheide, welche der Aussagen wahr sind.
Für unser heutiges Thema sehen wir uns zunächst die dritte Aussage etwas genauer an. Über Graphen von Funktion ersten (linear) und zweiten (quadratisch) Grades kannst du bereits genaue Aussagen treffen. Ab ganzrationalen Funktionen dritten Grades wird das schon schwieriger.
Skizziere in der folgenden Übung in die Vier Quadrate mögliche Verläufe von ganzrationalen Funktionen dritten Grades.
Tipp: Lässt man das Koordinatensystem in der Zeichnung weg, ergeben sich im Allgemeinen vier verschiedene Verläufe von Funktionsgraphen dritten Grades.
mögliche Verläufe für Polynomfunktionen dritten Grades
nützliche Info
Hier erfährst du noch kurz, wie dir der CAS bei Polynomfunktionen helfen kann. Dazu gibt es drei wichtige Befehle.
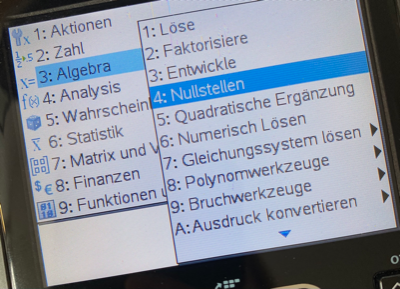
menu > 3: Algebra > 4: Nullstellen
In die Klammern tippst du einfach den Funktionsterm oder die zuvor definierte Funktion, z.B. f(x). Auch hier musst du wieder die jeweilige Variable (Argument) angeben.
Beispiel: zeros(3x+x,x)
Das Ergebnis wird dir in Mengenschreibweise, also mit {...} angegeben.
Übrigens kannst du genau so die solve-Funktion nutzen und den Term gleich Null setzen.
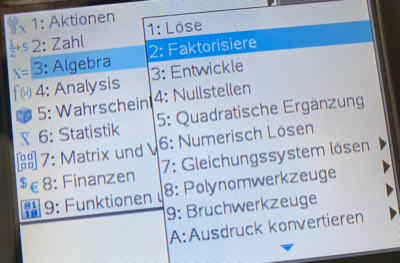
menu > 3: Algebra > 2: Faktorisiere
In die Klammern tippst du einfach den Funktionsterm oder die zuvor definierte Funktion, z.B. f(x).
Beispiel: factor(3x+x2)
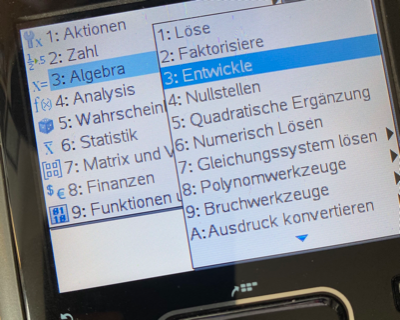
menu > 3: Algebra > 3: Entwickle
Dieser Befehl multipliziert für dich aus. In die Klammern tippst du einfach den Funktionsterm oder die zuvor definierte Funktion, z.B. f(x).
Beispiel: expand(x(3+x))
Bis hier hin solltest du bis zur Videokonferenz kommen. In dieser bearbeiten wir in Gruppen das folgende Arbeitsblatt.
