Taudin testaus
Pohditaan tapausta, jossa erään maan ihmisiltä testataan, onko heillä jokin tietty virus. Tapausta pohditaan kahden strategian näkökulmasta; toinen on "naiivi" ja suoraviivainen, joka maksaisi maltaita. Toinen on fiksummin pohdittu, ja tulee huomattavasti halvemmaksi. Juuri tämänkaltaisessa työssä, jonkun "optimin" löytämisessä, derivaatat tulevat usein käyttöön.
Koko maan väestöltä otetaan verinäytteet, ja testataan jokaisesta näin saadusta näytteestä havaitaanko siinä tätä virusta. Tartunta on melko harvinainen; sanotaan että tartunnan saaneita on väestöstä tasan yksi prosentti. Jos populaation koko on , ja yhden testin hinta on , saataisiin kokonaiskustannukseksi ``naiiville strategialle'', eli sille, että jokainen näyte eriskeen testataan, yksinkertaisesti .
Nyt kun tartunta on niinkin harvinainen, naiivi strategia ei ole rahallisesti järkevä. Sen sijaan jaetaan verinäytteet :n näytteen kokoisiin ryhmiin, yhdistetään ryhmän näytteet samaan astiaan, ja testataan se. Jos tulos on negatiivinen, voidaan kaikki sen ryhmän ihmiset kirjata negatiivisiksi. Jos tulos on positiivinen, testataan sen ryhmän ihmisten näytteet vielä jokainen erikseen. Kun -populaatioinen kansa jaetaan :n kokoisiin ryhmiin, tulee ryhmien määräksi (testauksen #1 vaiheessa):
Kutsutaan todennäköisyyttä sille että (yhdestä henkilöstä otetussa) näytteessä on tartunta symbolilla , ja vastaavasti terveen näytteen (ei tartuntaa) todennäköisyyttä . Nyt todennäköisyys sille, että ainakin joku testattavassa ryhmässä kantaa tartuntaa on
.
Yllä nähtävän päätelmän tekoon tarvitaan myös todennäköisyysmatematiikan perustietämystä.
Testauksen ykkösvaiheessa siis testattiin kaikki ryhmänäytteet. Sen jälkeen, testauksen toisessa vaiheessa, pitää vielä testata kaikki ihmiset erikseen niistä ryhmistä, joiden ryhmänäyte kantoi virusta.
Odotusarvo määrälle testejä mikä täytyy suorittaa testauksen toisessa vaiheessa on nyt
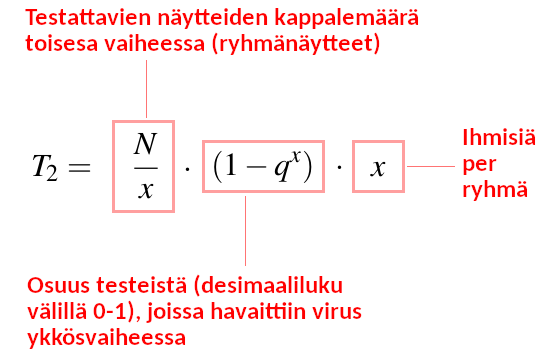
Nyt, voimme kirjoittaa tämän "fiksun" strategian testien odotusarvo on siis muotoon
.
TEHTÄVÄ:
Etsi ryhmän koko joka minimoi sen määrän testejä, joka on yhteensä tehtävä, eli etsi, millä :n arvolla saa minimiarvonsa.
VASTAUS:
Tässä vaiheessa on mielenkiintoista huomata, että vaikka emme tunne populaation kokoa , sillä ei ole väliä. Optimaalinen ryhmän koko ei riipu populaation koosta. Piirretään tästä derivaatasta kuva, ja katsotaan milloin se menee nollaksi.
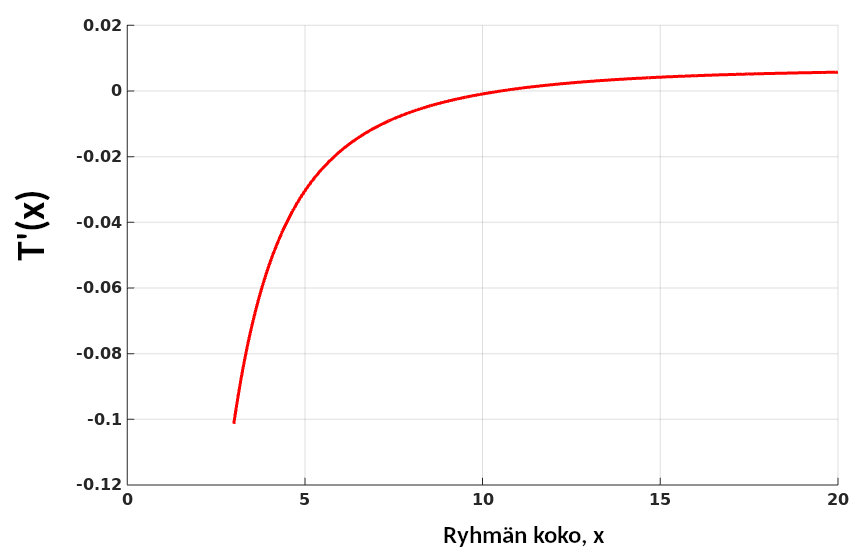
Kuvasta nähdään, että derivaatta menee nollaksi suunnilleen kohdassa . Koska
:n on oltava kokonaisluku, lasketaan :n arvot kun ja . Näistä pienempi on .
Jotta tehtävässä saadut havainnot eivät jää liian teoreettisiksi, kiinnitetään muutama luku reaalimaailmaan pohjautuvilla arvioilla, ja katsotaan mitä saadaan. Jos maan väkiluku (testattavien ihmisten kokonaismäärä) on , ja yhden testin hinta , niin silloin naiivin strategian hinnaksi tulee
,
siis 150 miljoonaa. Vastaavasti fiksulle stragetialle tulee kustannuksia
eli vähän vajaa miljoona. Huomataan, että tässäkin tapauksessa matematiikkaa hallitsevan ihmisen pitäminen palkkalistoilla on hintansa arvoista!