Tutoria em Matemática Básica - Aula 07


Função Polinomial do 1º grau e Inequação do 1º grau
Olá, alunos!
Nessa aula
estudaremos o conteúdo de Função Polinomial do 1º grau, ou ainda, Função Afim e ao final, as inequações do 1º grau. Para iniciar essa aula, apresentaremos uma situação inicial como motivação para o estudo desse tipo de função.
Considere a situação abaixo:
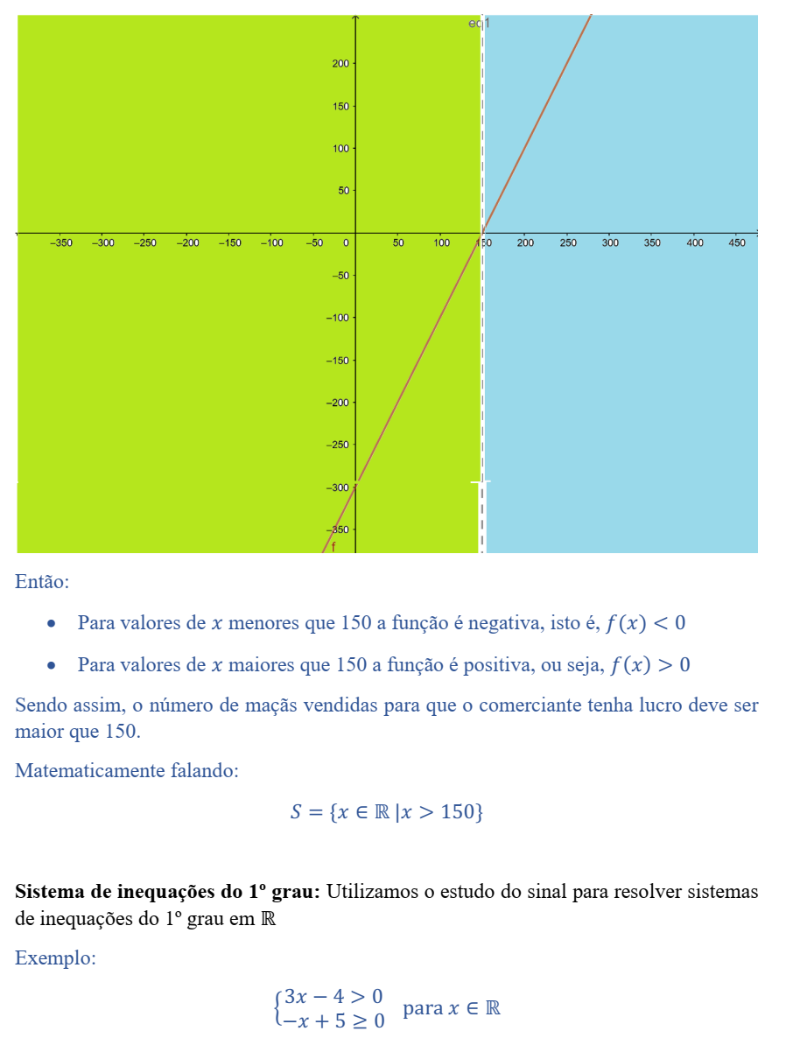
Um representante comercial recebe, mensalmente, um salário composto de duas partes: uma parte fixa, no valor de R$ 2.500,00 e uma parte variável que corresponde a uma comissão de 6% sobre o total de vendas que ele faz durante o mês. Nessas condições, podemos dizer que:
Onde: A variável S representa o salário desse representante em um determinado mês e a variável v corresponde ao total de vendas desse representando no mês em questão. Note que o salário do representante depende do total de vendas feitas por ele, então podemos reescrever essa expressão como:
Esse é um exemplo de Função Afim.
Função Afim:
Sejam a, b números reais, sendo . Chamamos de Função Afim (ou Função Polinomial do 1º grau) a função definida por para todo .
Exemplos:
a) , com a = 2 e b = 4
b) , com a = -1 e b = 7
c) , com e b = -8
Coeficientes de uma função afim: Seja f uma função afim, tal que f(x)=ax+b, com . Chamamos os números reais a e b de coeficientes, sendo:
- O coeficiente a é dito coeficiente angular
- O coeficiente b é dito coeficiente linear
Observação:
Geometricamente, é a ordenada do ponto onde a reta que representa o gráfico da função f(x) = ax + b intercepta o eixo y, pois para x = 0, temos que: f(0) = a . 0 + b = b
Taxa de variação da função afim:
Abra o arquivo a seguir e movimente os controles deslizantes e o ponto A. Observe o que ocorre com os valores de m, n e t conforme movimentamos os controles deslizantes a, b e h.
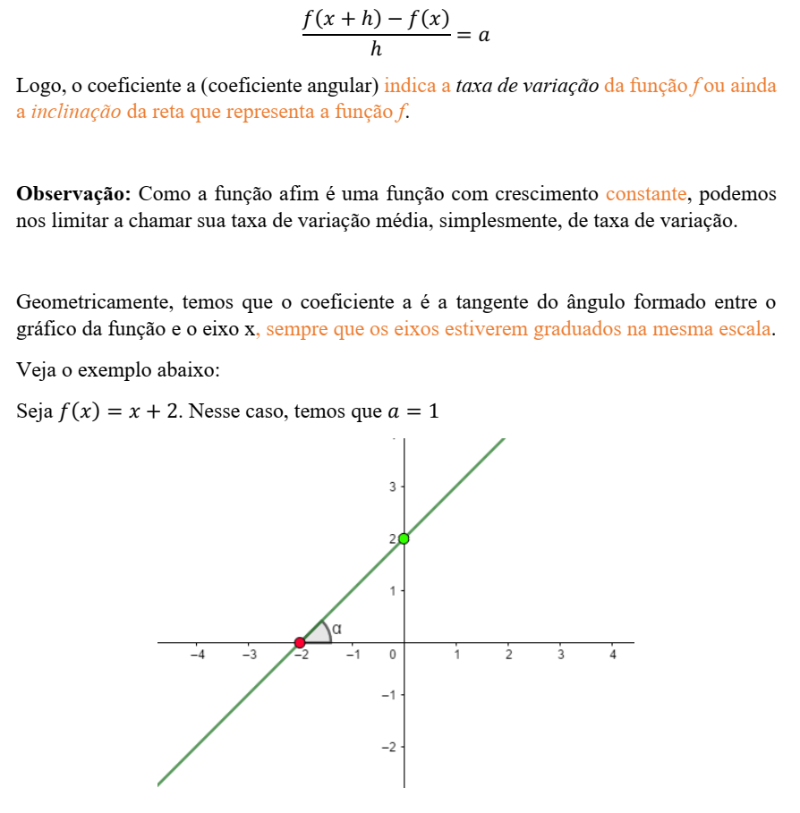
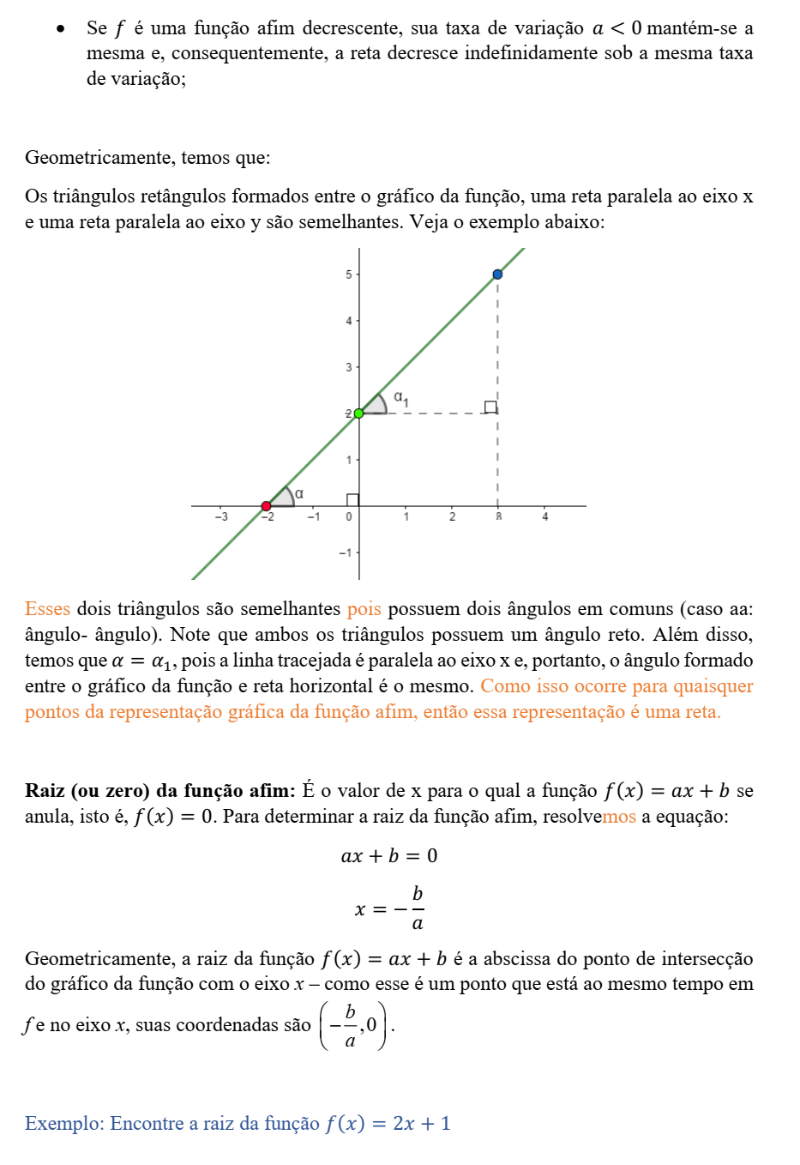
A esse valor que denominamos por t chamamos de taxa de variação da função f. Esse valor se relaciona com a variação de crescimento da função ao longo de seu domínio. Conforme podemos observar manipulando a função, fixando os valores a e b, ou seja, para uma função afim específica qualquer, o valor de t não varia e, além disso, ele é numericamente igual ao valor do controle deslizante a. O objeto geométrico que tem crescimento constante é uma reta – e é por essa razão que o gráfico de uma função afim é sempre representado por uma reta. Mais formalmente, temos: