体と群は表裏一体
1.かきまぜても不変な部分に着目しよう
このワークシートはMath by Codeの一部です。
前回は
f(x)の最小分解体Kを使った代数拡大K/Qをガロア群G(f/Q)
とガロア群を定義したね。
もとの数体をQに限定せずに、一般化して定義してみよう。
不変体に着目
<不変体は中間体>
・代数拡大L/KでLの部分体LHは、体Kの自己同型群(G=Aut(K))の部分群Hで不変な体。
つまり、かきまぜ方の1つHを体Lに作用させても動かない部分のことだね。
KそのものはどのHでも不変だから、不変体はL/Kの中間の体になる。
<中間体と部分群は表裏一体>
部分群HをG全体にすると、LG=Kなら、L/Kは正規拡大(ガロア拡大)という。
このときG=Gal(L/K)=Aut(L/K)を、LのK上のガロア群という。次数は[L:K]=|G|。
(例)
Qが不変体で、ガロア群がAut(L/Q)、L/Qがガロア拡大になる例
・f(x)=x2-2の最小分解体L=Q(√2)。ガロア群=S2。
・f(x)=x4-10x-1の最小分解体L=Q(√2+√3)。ガロア群=V4。
・f(x)=x3-2の最小分解体L=Q(ω, ) 。ガロア群=S3。
(例)
ガロア拡大でない例
・f(x)=x3-2に対して、L=Q( ) ={p+q +r 2 |p,q,r∈Q}とする。
Aut(L/K)={e}だった。拡大したあとの全体がまるごと動かない。
つまり、LQ=Lになってしまうから、ガロア拡大でもガロア群でもない。
「拡大したところが動いて、拡大のもとが動かない」
という2層化がガロア拡大のイメージと言えるね。
最小分解体L=Q(√2,√3)のガロア群はV4
2.体の拡大の流れと部分群の流れは逆転する
<ガロア拡大とガロア群の包含関係の逆転>
L/KがQの拡大体によるガロア拡大で、G=Gal(L/K)とする。
・MがL/Kの中間体ならL/Mもガロア拡大で、Mを不変にする群は部分群H=FixG(M)<G。
・Gの部分群HはM=LHを不変にする。MはL/Kの中間体。
中間体の集合をM、部分群の集合をHとするとき
*:M→H、¥:H→Mとすると、
・Gの部分群hと中間体mの一対一対応がある。
中間体m∈Mに対してはm*はLのすべての自己同型群。
部分群h∈Hに対してはh¥はhの不変体。
・Gの部分群hと中間体mの一対一対応は、包含関係を逆転させる。
m1<m2∈Mなら、m1*>m2*∈H
だから、
K*=G, M*=H,L*={e}
つまり、富士山の頂上の体Kから中間体Mが続き、そこから麓の体Lへと流れがある。
「富士山の体」のこの拡大体の流れ K<Ms<L に対して、
逆さ富士では、Kを不変にする群G、次にMを不変にする群Hが続き、Lを不変にする群{e}とつながる。
「逆さ富士の群」の部分群の流れ G>Hs>{e} が対応す
つまり、富士山の頂上の体Kから中間体Mが続き、そこから麓の体Lへと流れがある。
・[L:K]=|G|の中間体をMとする。M*が自己同型群Gの部分群。
[L:M]=|M*|
[M:K]=|G|/|M*|
もしも|G|=6、|M*|=3ならば、Mを基底とするLの拡大次数[L:M]も3。
[M:K]=|G|/|M*|=6/3=2だから、Lを基底としたMの次数は2となる。
言い換えると、|G|=[L:K]=[L:M][M:K]=|M*|[M:K]だから、|M*|と|M:K|は反比例する。
だから、体の拡大のハッセ図と群の部分関係のハッセ図を
対応させて書くと、対応する位数の積は一定になる。
[L:K][L*]=[L:K][{e}]=|G|
[M:K][M*]=[L:K][H|=|G|
[K:K][K*]=[K:K]|G|=|G|
(例)
f(x)=(x2-2)(x2-3)の分解体Lのガロア群Gの部分群と対応するLの中間体は?
分解体L=Q(√2,√3)={a+b√2+c√3+d√6 | a,b,c,d∈Q}
ガロア群G=Gal(L/Q)=V4=Z/2Z×Z/2Z={(0,0),(0,1),(1,0),(0,0)}={e,p,q,r=pq}
p(√2)=-√2,p(√3)=√3,q(√2)=√2,q(√3)=-√3。
pq(√6)=pq(√2*√3)=p(√2*(-√3))=(-√2)(-√3)=√6
Gの自明でない部分群H={A,B,C}={{e,p},{e,q},{e,r}}の3個でどれも位数は2。
対応する中間体H=LA,LB,LCとすると、LA=Q(√3),LB=Q(√2),LC=Q(√6)。
拡大次数は[L:H]=[H:L]=2
(例)
f(x)=x3-2の分解体Lのガロア群の部分群と対応するLの中間体は?
u1,u2,u3= , ω , ω2 とおくと、
分解体L=Q( ,ω)=Q({a+bω+c +dω +e 2+fω 2 | a,b,c,d,e,f∈Q}= Q(u1,u2,u3)。
ガロア群G=Gal(L/K)=S3={e, s:(1 2 3), ss:(1 3 2), a:(1 2) , b:(1 3) ,c :(2 3)} [L:K]=6
Gの自明でない部分群H={A,B,C,N}={{e,a},{e,b},{e,c},{e,s,ss}}の4個で位数は2か3。
だから、拡大次数[H:Q]=2か3。
u1,u2,u3はそれぞれ、互換c(2 3),b(1 3),a(1 2)で不変だとすると対応する中間LC,LB,LA=Q(u1),Q(u2),Q(u3)。
自明でない中間体M=Q(ω)はωが2次方程式の解で[M:Q]=2だから、[L:M]=6/2=3となりNの次数に一致する。LN=Q(ω)。N={e,r,s}は正規部分群。
質問:ガロア対応を視覚化するコードはどうかけばよいでしょうか。
群のハッセ図をhasseGでかきます。
表示するためのデータを{ノード名:表示ラベル}の辞書形式itemsで渡します。
位数のデータをsizeで渡します。
そのあとG.node()でitemsをノードにしてグラフにつけましょう。
最後にitemsを→でつなぐために、2つのノード(群)の位数sizeを
読み取って割り切れてしかも、divCount==2(素数)のときだけつなぎます。
つなぎ方は小から大へ→が出るようにするので、
単位元が一番上、Gが一番下、中間に部分群がきます。
→には位数の商(指数)をつけましょう。
体のハッセ図はhasseKでかきます。
体のハッセ図を群のハッセ図に対応させて書くと、対応する位数の積は一定になる。
[L:K][L*]=[L:K][{e}]=|G|
[M:K][M*]=[L:K][H|=|G|
[K:K][K*]=[K:K]|G|=|G|
位数データは群と同じものを渡しますが、
上下を逆にかくために、
自明でない部分群の位数はGの位数を割って反転させます。
Qを基底とした拡大の次数のデータとして使います。
上下逆にするので、Lが一番上、Qが一番下、中間に中間体がきます。
→には拡大次数をつけますが、→が縮小みたいで、何か変ですね。。。。
dir属性を逆にすると改善できます。
import graphviz
from itertools import permutations
def hasseG(items,size):
G = graphviz.Digraph()
for k, v in items.items():
G.node(name = str(k), label =v )
nodes = items.keys()
M = list(range(2,len(items)))
divCount = lambda n:len(list(filter(lambda m:n % m==0, list(range(1,n+1)))))
P = [x for x in M if divCount(x)==2]
for pm in permutations(items,2):
x,y = pm
a,b = size[x],size[y]
div = a//b
if a % b ==0 and (div in P):
G.edge(str(y),str(x),str(div)) #上が小y、下が大x(群)
return G
def hasseK(items,size):
mins = min(size)
maxs = max(size)
recipro = lambda x: maxs//x if (x!=mins and x!=maxs) else x #拡大次数のために個数を反転させる。
size=[recipro(x) for x in size]
G = graphviz.Digraph()
for k, v in items.items():
G.node(name = str(k), label =v )
nodes = items.keys()
M = list(range(2,len(items)))
divCount = lambda n:len(list(filter(lambda m:n % m==0, list(range(1,n+1)))))
P = [x for x in M if divCount(x)==2]
for pm in permutations(items,2):
x,y = pm
a,b = size[x],size[y]
div = a//b
if a % b ==0 and (div in P):
G.edge(str(x),str(y),str(div),dir='back') #上が大x、下が小y
return G
#=====================================================
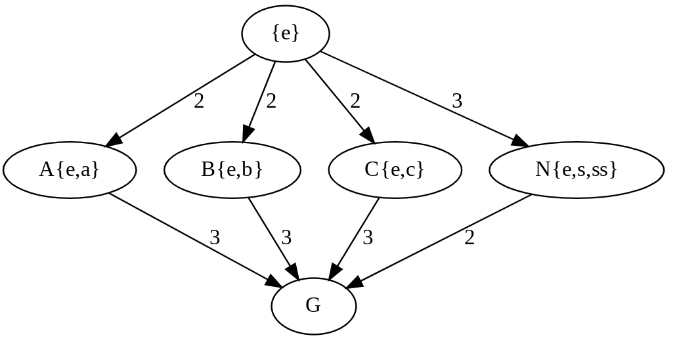
items={0:"{e}",1:"A{e,a}",2:"B{e,b}",3:"C{e,c}",4:"N{e,s,ss}", 5:"G"}
size=[1,2,2,2,3,6]
G = hasseG(items,size)
G
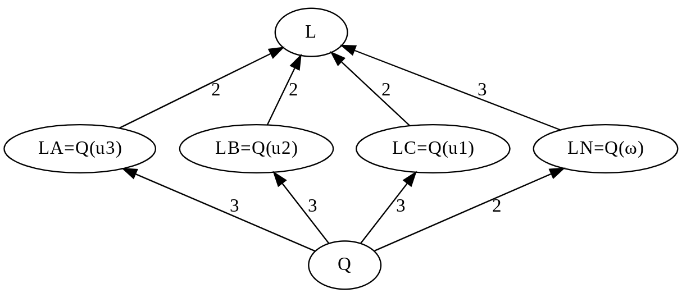
items={0:"Q",1:"LA=Q(u3)",2:"LB=Q(u2)",3:"LC=Q(u1)",4:"LN=Q(ω)", 5:"L"}
size=[1,2,2,2,3,6]
K = hasseK(items,size)
K
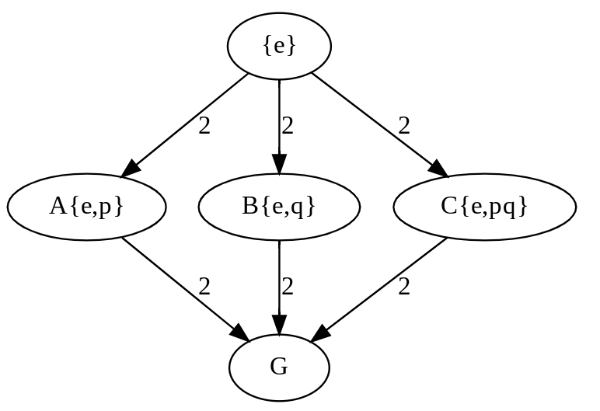
items={0:"{e}",1:"A{e,p}",2:"B{e,q}",3:"C{e,pq}",4:"G"}
size=[1,2,2,2,4]
G = hasseG(items,size)
G
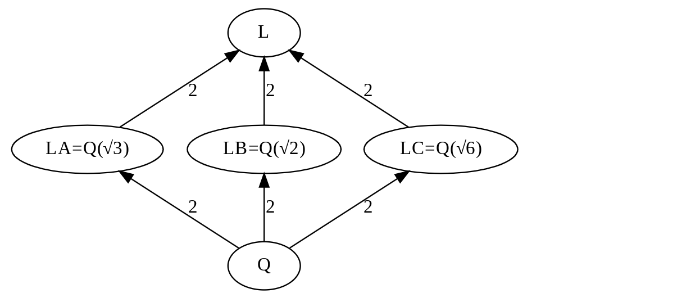
items={0:"Q",1:"LA=Q(√3)",2:"LB=Q(√2)",3:"LC=Q(√6)",4:"L"}
size=[1,2,2,2,4]
K = hasseK(items,size)
K