Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Lesson 3; Balanced Moves

Author:Arpit Kesharwani

Warm Uo

Figures A, B, C, and D show the result of simplifying the hanger in Figure A by removing equal weights from each side.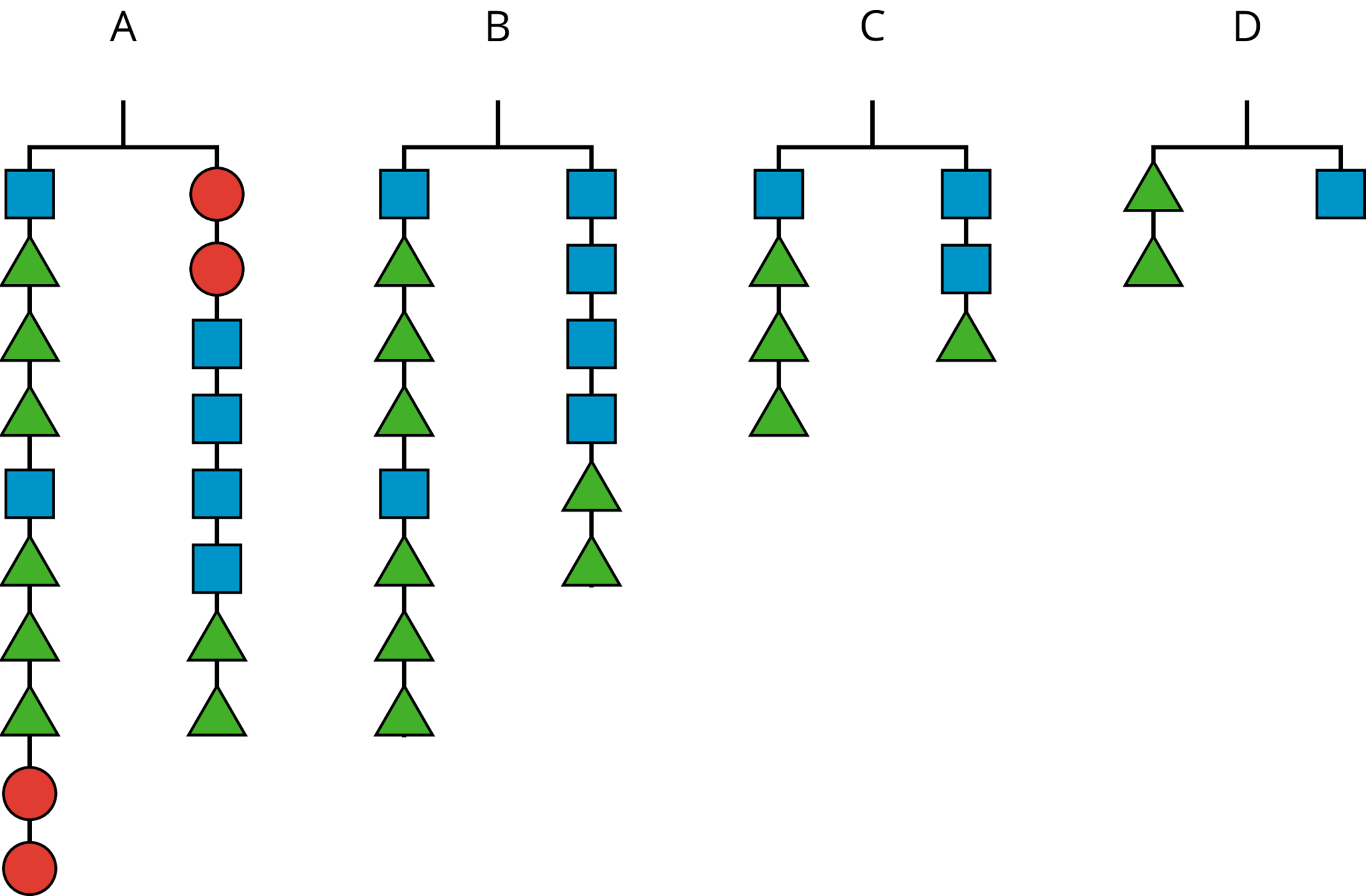 Here are some equations. Each equation represents one of the hanger diagrams.2(x+3y)=4x+2y2y=x2(x+3y)+2z=2z+4x+2yx+3y=2x+y

  1. Write the equation that goes with each figure: A: B: C: D:
  2. Each variable (x, y, and z) represents the weight of one shape. Which goes with which?
  3. Explain what was done to each equation to create the next equation. If you get stuck, think about how the hangers changed.

Check my answer

Gettin' your Hands Dirty

MaterialsIF YOU CAN'T ACESS THE CLASSROOM ACTIVITY PLEASE GO TO THIS LINK; https://im.openupresources.org/8/teachers/materials/4/3/8-4-3-2-blackline_master.pdf In this activity, students match a card with two equations to another card describing the move that turns the first equation into the second. The goal is to help students think about equations the same way they have been thinking about hangers: objects where equality is maintained so long as the same move is made on each side. Additionally, this is the first activity where students encounter equation moves involving negative numbers, which is not possible when using hangers. Launch Review with students what we know about equations based on reasoning about hangers:
  • We can add the same quantity to each side, and the equation is still true (the hanger is still in balance).
  • We can subtract the same quantity from each side, and the equation is still true.
  • We can double or triple or halve or third the things that appear on each side, and the equation is still true. More generally, we can multiply the number of things on each side by the same number.
Tell students that hanger diagrams are really only useful for reasoning about positive numbers, but the processes above also work for negative numbers. Negative numbers are just numbers, and they have to follow the same rules as positive numbers. In fact, if we allow negative numbers into the mix, we can express any maneuver with one of two types of moves:
  • Add the same thing to each side. (The “thing” could be negative.)
  • Multiply each side by the same thing. (The “thing” could be a fraction less than 1.)
Arrange students in groups of 2. Give each group 12 pre-cut slips from the blackline master. Give 3–4 minutes for partners to match the numbered slips with the lettered slips then 1–2 minutes to trade places with another group and review each other’s work. Ask partners who finish early to write down on a separate sheet of paper what the next move would be for each of the numbered cards if the goal were to solve for x. Follow with a whole-class discussion.

Student Facing Assignments

Your teacher will give you some cards. Each of the cards 1 through 6 show two equations. Each of the cards A through E describe a move that turns one equation into another.

  1. Match each number card with a letter card.
  2. One of the letter cards will not have a match. For this card, write two equations showing the described move.

Check my answer

Activity Summary

The goal of this discussion is to get students using the language of equations and describing the changes happening on each side when solving. Ask:
  • “What is a move you could do to the equation 7=2x on card 1 that would result in an equation of the form x=⎯? What is another move that would also work?” (Multiply each side by 12. Divide each side by 2.)
  • “Which numbered card was the most challenging to match?” (Card 2, because it at first I only looked at the x-terms and thought the move involved a change of 8x.)
  • “Does anyone have a value for x that would solve one of the numbered cards? How did you figure it out?” (x=2 is a solution for card 5. I added 3 to each side and then multiplied each side by 14.)
End the discussion by inviting groups to share the equations they wrote for card 6 and describe how they match the move "add 3x to each side."

Activity; Try the dilations on this grid.

Activity Overview

The purpose of this activity is to get students thinking about strategically solving equations by paying attention to their structure. Distribution first versus dividing first is a common point of divergence for students as they start solving.Identify students who choose different solution paths to solve the last two problems. Arrange students in groups of 2. Give students 2 minutes quiet think time for problem 1, then 3–5 minutes partner time to discuss problem 1 and complete the other problems. Follow with a whole-class discussion.

  1. Noah and Lin both solved the equation 14a=2(a−3).Do you agree with either of them? Why?Noah's solution:14a14a12aa=2(a−3)=2a−6=-6=-12Lin's solution:14a7a6aa=2(a−3)=a−3=-3=-12
  2. Elena is asked to solve 15−10x=5(x+9). What do you recommend she does to each side first?
  3. Diego is asked to solve 3x−8=4(x+5). What do you recommend he does to each side first?

Check my answer

New Resources

Discover Resources

Discover Topics