Wiederholung von Extremwertproblemen
Lösungsschritte mit Beispiel
Beim Lösen von Extremwertproblemen kommt man mithilfe von vier Schritten auf das Ergebnis:
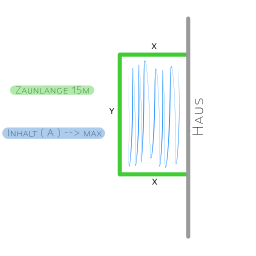
Als Beispiel dient uns eine Hauswand wie im Bild oben zu sehen.
Die Aufgabe ist es, den größt möglichen Flächeninhalt zu zu errechnen, den man mit 15 m Zaun erreichen kann.
Schritt 1 :
Aufstellen eines Funktionsterms für die gesuchte Größe. ( in diesem Fall A )
A = x * y
Schritt 2 :
Aufstellen einer Gleichung, die die Nebenbedingung beschreibt und diese umstellen.
2x + y = 15 (Nebenbedingung Zaunlänge) ---> y = 15 - 2x
Schritt 3 :
Einsetzen der umgeformten Funktion in y und ausmultiplizieren.
A (x) = x * ( 15 - 2x ) ----> A (x) = 2x² + 15x
Schritt 4 :
Ermittlung des Scheitelpunkts und Angabe des Extremwerts
Nullstellen : x * (15 - 2x ) = 0
x ₁ = 0 x₂ = 7,5
Scheitelpunkt : ( x₁ + x₂ ) / 2
( 0 + 7,5 ) / 2 = 3,75
Extremwert : 15 - 2 * 3,75 = 7,5
x = 3,75 y = 7,5
A = 3,75 * 7,5 = 28,125 [m²]