13- Desafios Finais
86) DESAFIO 1: ENEM (2018)
Minecraft é um jogo virtual que pode auxiliar no desenvolvimento de conhecimentos relacionados a espaço e forma. É possível criar casas, edifícios, monumentos e até naves espaciais, tudo em escala real, através do empilhamento de cubinhos.
Um jogador deseja construir um cubo com dimensões 4 x 4 x 4. Ele já empilhou alguns dos cubinhos necessários, conforme a figura.
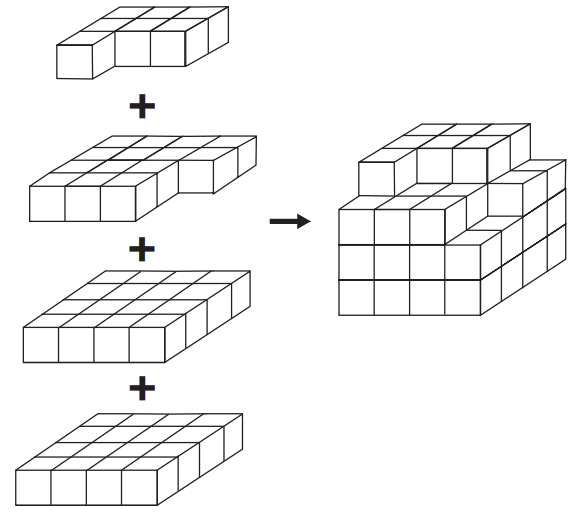
Os cubinhos que ainda faltam empilhar para finalizar a construção do jogo, juntos, formam uma peça única, capaz de completar a tarefa.
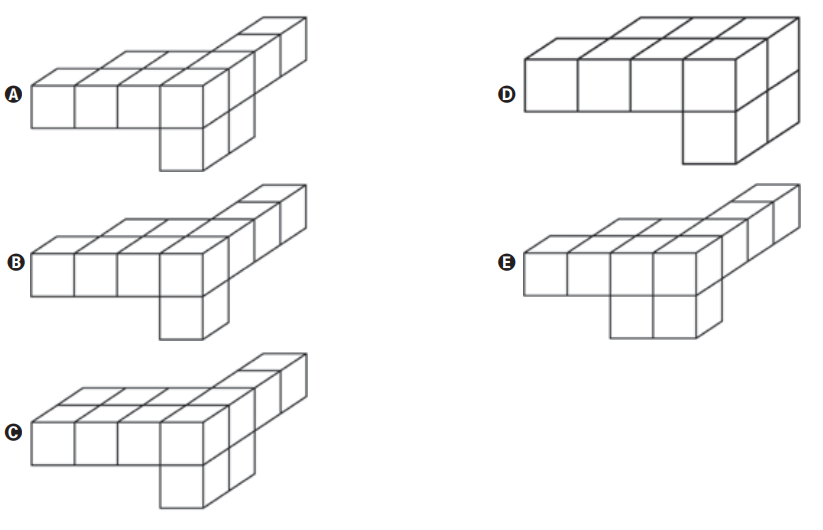
Marque a alternativa que corresponde ao formato da peça capaz de completar o cubo 4 x 4 x 4.
Vink alles aan wat van toepassing is
- A
- B
- C
- D
- E
87) DESAFIO 2: adaptado de ENEM (2020)
A Figura 1 apresenta uma casa e a planta do seu telhado, em que as setas indicam o sentido do
escoamento da água de chuva. Um pedreiro precisa fazer a planta do escoamento da água de chuva de um telhado que tem três caídas de água, como apresentado na Figura 2.
![[size=150]A figura que representa a planta do telhado da[b] Figura 2[/b] com o escoamento da água de chuva que o pedreiro precisa fazer é[/size]](https://www.geogebra.org/resource/ugvahhqc/LetkbggJrgczuuTT/material-ugvahhqc.png)
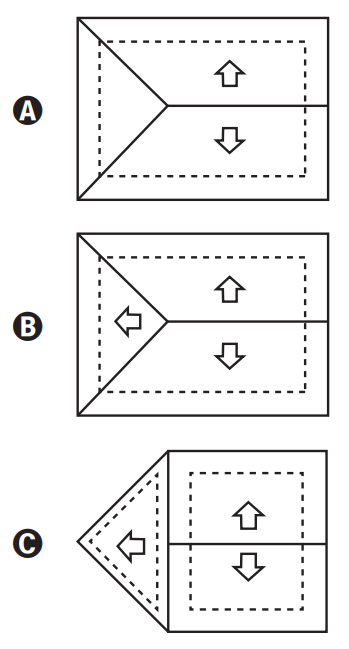
Marque a alternativa correta
Vink alles aan wat van toepassing is
- A
- B
- C
88) DESAFIO 3: adaptado de Fundação Liberato (2017)
Em 2017 a Fundação Liberato comemora 50 anos de existência. Para homenagear a escola, a aluna Eduarda fará uma pintura do logotipo da Fundação Liberato (conforme figura 1). Essa pintura será feita em apenas uma das faces de um quadro de vidro incolor, de modo que, pela transparência do vidro, seja possível visualizar o logotipo no verso do quadro.
![[size=150]Considerando que cada alternativa ilustra, primeiramente, a face pintada (vista frontal) e, em seguida, o verso (vista de trás) dessa pintura, a alternativa que melhor representa a maneira como o logotipo poderá ser visto dos dois lados é[/size]](https://www.geogebra.org/resource/w7vxbctx/araYoS7SxLRHdUtq/material-w7vxbctx.png)
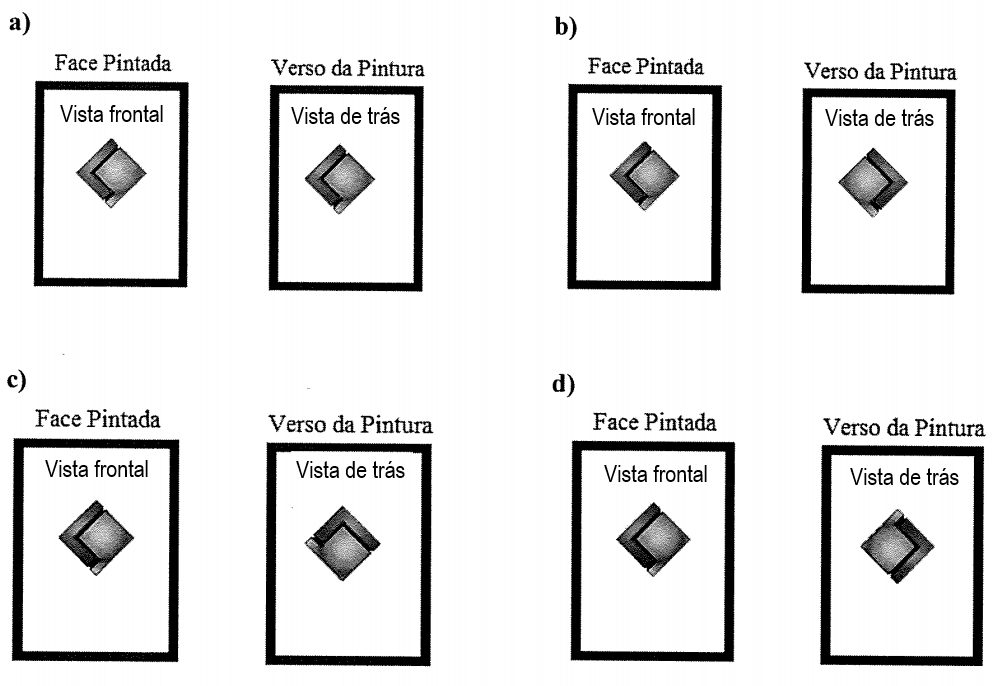
Vink alles aan wat van toepassing is
- A
- B
- C
- D
89) DESAFIO 4: observe a pilha de blocos retangulares e a caixa para responder as questões a, b e c a seguir.
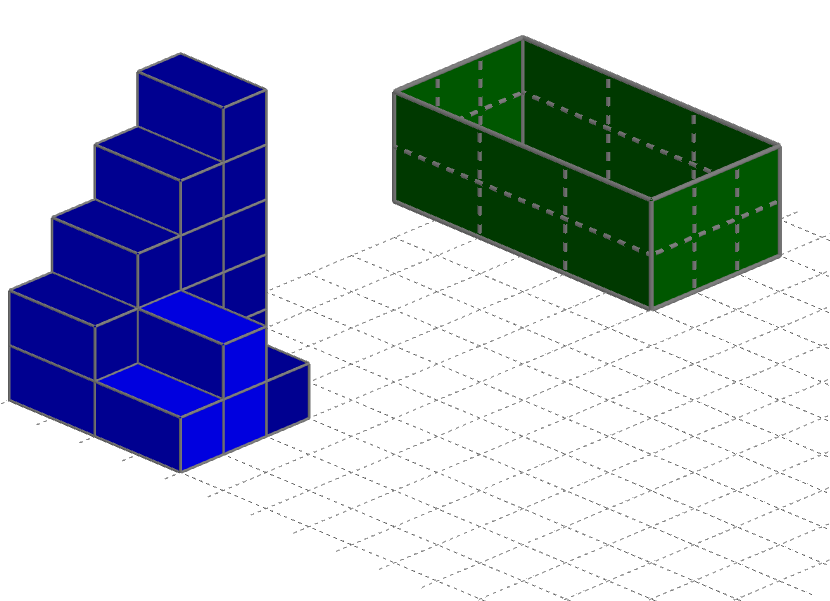
a) Qual é o número total de blocos retangulares que estão fora da caixa?
b) Qual o número máximo de blocos retangulares que cabem dentro da caixa?
c) Todos os blocos retangulares que estão fora da caixa cabem dentro dela?
Vink alles aan wat van toepassing is
- A
- B
90) DESAFIO 5: observe este sofá para desenhar o que se pede.
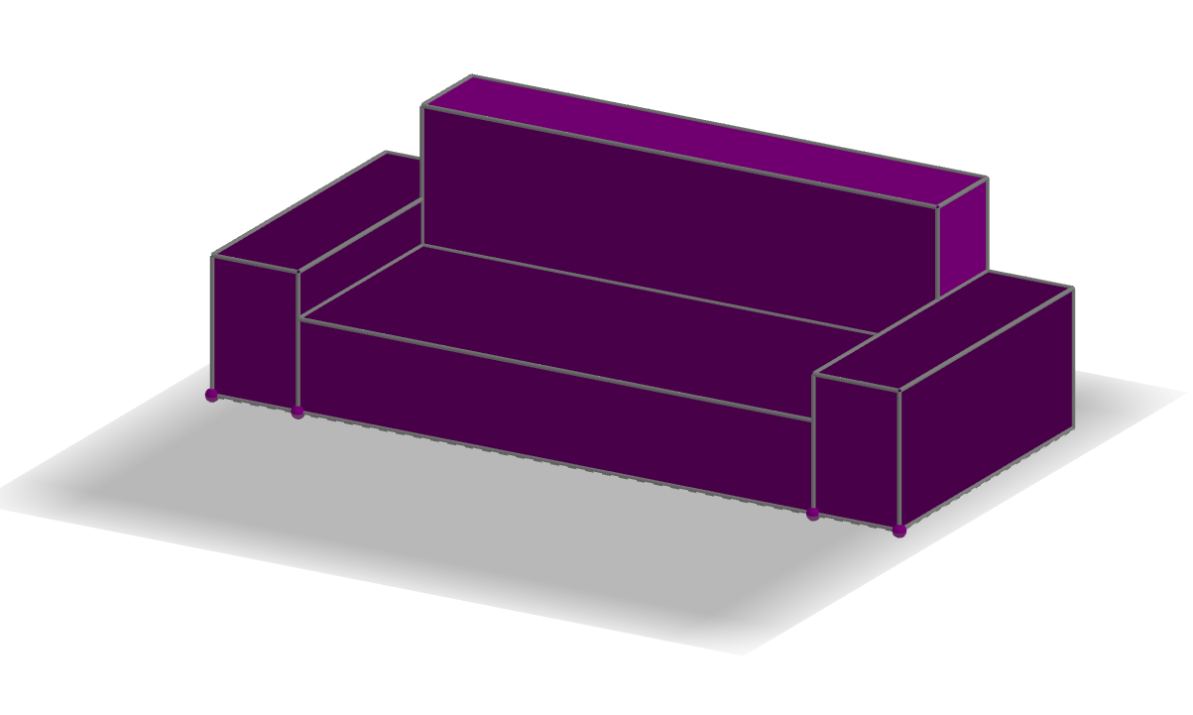
91) DESAFIO 6: CUBOS EM PERSPECTIVA
Desenhe os 4 cubos a seguir, utilizando a mesma linha do horizonte e o mesmo ponto de fuga. Apresente onde está a linha do horizonte e o ponto de fuga.
![[size=150][color=#ff0000]IMPORTANTE[/color]: lembre-se de tirar fotos do passo a passo e enviar para o professor.[/size]](https://www.geogebra.org/resource/r5kspwyu/WML3NXPV41UycRMo/material-r5kspwyu.png)